Perfect Euler Line
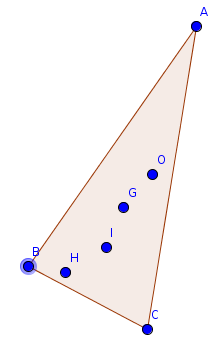
A non-equilateral has centroid , orthocenter , incenter , circumcenter that satisfy . Find the measure of the smallest angle, to the nearest degree.
Note : Figure not necessarily drawn to scale.
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Euler Line
The actual answer is 2 a r c s i n 4 1 , which is approximately 2 8 . 9 5 5 ° .
The first thing to realize is that the triangle is isosceles. O , G , H are always collinear with H G = 2 G O (Head to the wiki for more info). Therefore, in order to make H I = I G = G O , I must be halfway between H and G , indicating that the triangle is isosceles.
Without losing generality, let A be the vertex angle and the distance from H to B C be 1 . Let H I = I G = G O = x . As A G = 2 G O , A G = 4 x + 2 .
Make I K ⊥ A C , then I K = x + 1 , C O = 3 x + 2 . Pythagorean theorem yields C J = 6 x + 3 . Apply Pythagorean theorem another time and get A C = ( 6 x + 3 ) ( 6 x + 4 ) . Then s i n θ = ( 6 x + 3 ) ( 6 x + 4 ) 6 x + 3 = 6 x + 4 1 .
On the other hand, s i n θ = 5 x + 2 x + 1 . Let the equations equal and we get x = 2 . Plugging back yields s i n θ = 4 1 .
Therefore, m ∠ B A C = 2 a r c s i n 4 1 ≈ 2 9 ° < 6 0 ° , so it is the smallest angle thus this is the answer.