Perfect matching on a regular graph

Probability Level 5

In this problem, graphs are simple.

A matching on a graph G G is a subset of E ( G ) E(G) such that no two edges in the subset share an end. The size of a matching is the number of edges in it.

A perfect matching on a graph G G is a matching whose size is ⌊ ∣ V ( G ) ∣ 2 ⌋ \left\lfloor \frac{|V(G)|}{2} \right\rfloor ; that is, a matching that's as big as possible given the number of vertices.

For example, in the following image, the left graph shows a matching of size 2 2 . It is not perfect, and in fact it doesn't have a perfect matching. Adding an edge to give the right graph, however, gives a matching of size 3 3 and hence a perfect matching.

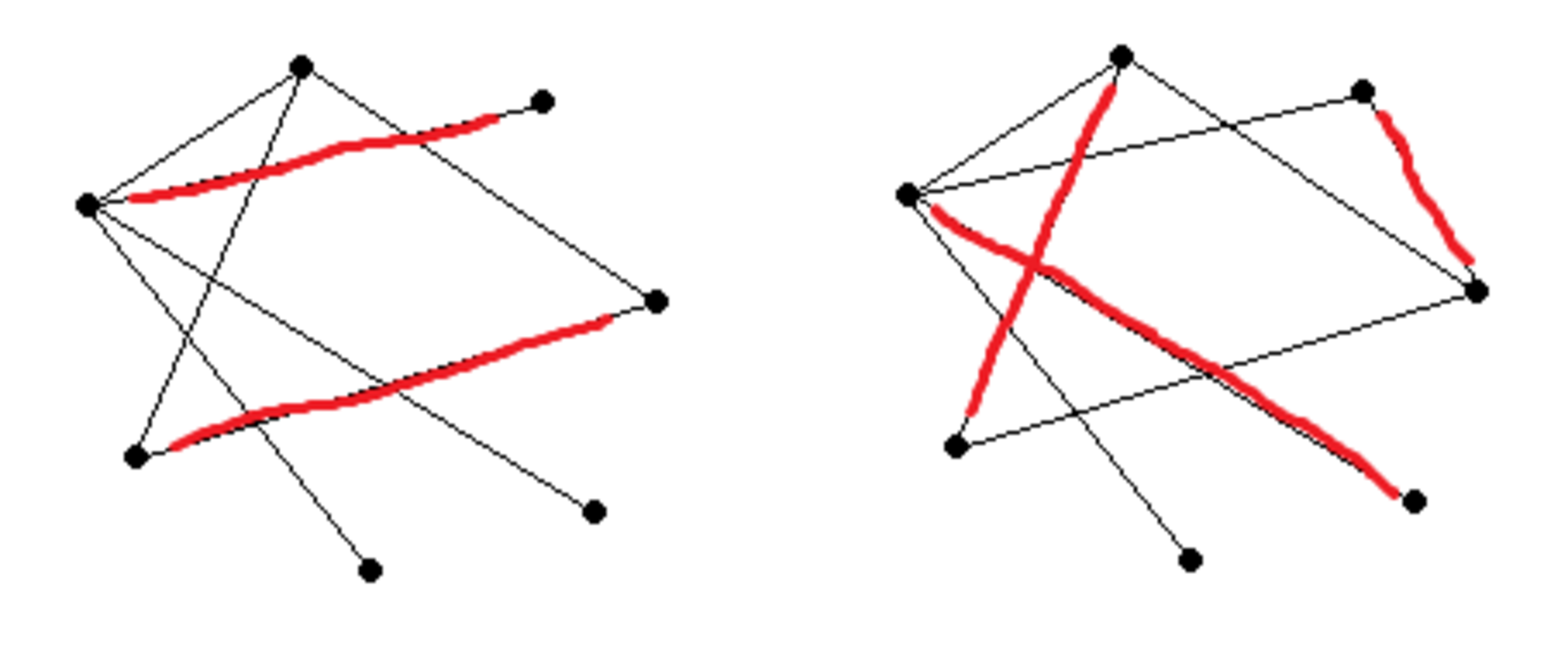
A k k -regular graph is a graph where every vertex has degree k k .

For 0 ≤ k ≤ 2015 0 \le k \le 2015 , how many values of k k make this statement true: "all k k -regular graphs have a perfect matching"?


The answer is 1.

View wiki
Ivan Koswara by Ivan Koswara , 25, Indonesia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ivan Koswara
Sep 17, 2015

Call two edges that share an end to be adjacent . Let V , E V,E be the set of vertices and edges of our graph respectively.

We claim that only k = 1 k = 1 makes the statement true.

First, k = 1 k = 1 is trivial: pick all the edges. Clearly no pair of edges will be adjacent. Additionally, by the degree sum formula , we have deg ⁡ v = 1 \deg v = 1 for all v v and thus ∣ E ∣ = 1 2 ∑ deg ⁡ v = 1 2 ∣ V ∣ |E| = \frac{1}{2} \sum \deg v = \frac{1}{2} |V| , which means our choice is indeed a perfect matching.

Next, k = 0 k = 0 is also trivial: the graph of two vertices and no edge is clearly 0 0 -regular and has no matching of size 1 1 (there's not even enough edges), so no perfect matching.

The real meat lies on proving for k ≥ 2 k \ge 2 that this doesn't hold either.

For even k k , consider the union of two copies of K k + 1 K_{k+1} . On a complete graph K n K_n , the degree of each vertex is n − 1 n-1 , thus on our graph the degree of each vertex is indeed ( k + 1 ) − 1 = k (k+1)-1 = k , so our graph is k k -regular. There are 2 ( k + 1 ) = 2 k + 2 2(k+1) = 2k+2 vertices, thus there should be k + 1 k+1 edges in a perfect matching. However, clearly no edge can cross between the two copies (there are no edges between them), so each edge in our matching uses two vertices in the same copy. By Pigeonhole Principle, one copy has at least ⌈ k + 1 2 ⌉ = k 2 + 1 \left\lceil \frac{k+1}{2} \right\rceil = \frac{k}{2} + 1 edges of the matching, and together they use 2 ( k 2 + 1 ) = k + 2 2 \left( \frac{k}{2} + 1 \right) = k+2 vertices (each edge uses two vertices, and no vertex can be used twice since it's a matching), contradicting the fact that each copy only has k + 1 k+1 vertices. This rules out the even k k .

For odd k k , the situation is a little more complicated.

First, consider the complete graph K k + 1 K_{k+1} again. We can easily obtain a perfect matching here (pick any edge not adjacent to previously selected edges; rinse and repeat until you're done). Now keep any one edge from the matching, and delete the rest. This makes k − 1 k-1 of the vertices to have degree k − 1 k-1 . Now introduce a new vertex u u and connect it to each of these k − 1 k-1 vertices. Now we have a graph G ′ G' on k + 2 k+2 vertices, where k + 1 k+1 vertices have degree k k and one (namely u u ) has degree k − 1 k-1 .

Make k k copies of G ′ G' and introduce one new vertex v v . Join v v with each of the k k copies of u u . Now each of the u u 's has degree k k , and v v also has degree k k , so our graph is k k -regular.

We will prove this graph doesn't have a perfect matching.

The proof is quite simple. Note that there are ( k + 1 ) 2 (k+1)^2 vertices in total, which is even, so all vertices are used in the matching. Consider the vertex connected to v v in the matching. This must be connected to one of the u u vertices. Removing the two vertices breaks the graph into several components.

By our construction, there will be k − 1 k-1 copies of G ′ G' that are still intact. Since k ≥ 2 k \ge 2 , we have k − 1 ≥ 1 k-1 \ge 1 , so there is at least one copy unused. Each of these copies have k + 2 k+2 vertices, an odd number, and thus one must remain unused in the matching. But as proved above, in order to have a perfect matching, all the vertices must be used, contradiction.

Thus all k ≥ 2 k \ge 2 doesn't satisfy the statement. There is only 1 \boxed{1} value of k k that makes the statement true.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Interesting construction with the odd k k case. How did you think of it? To what extent could it be motivated from the conditions?

A slightly easier way to define G ′ G' , is to take K k + 2 K_{k+2} , choose a vertex v 1 v_1 , remove all vertices of the form v 1 v i v_1 v_i where i ≠ 2 , k + 2 i \neq 2, k+2 , and then remove v 2 v k + 2 v_2 v_{k+2} .

Challenge Master: To be honest, this construction is actually inspired from my professor's; the case k = 3 k=3 actually gives the exact same construction. He was teaching on how 3-regular graphs don't necessarily have a perfect matching (but they do if you restrict to graphs with no more than 2 cut edges), and I generalized the construction.

I don't see how the proposed G ′ G' has no perfect matching. Just include v 1 v 2 v_1 v_2 and the remaining graph is K k K_k which clearly has a perfect matching.

Ivan Koswara - 5 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...