Perfect notes
Two musical notes are harmonious (sound great together) if the ratio of the frequencies corresponds to the ratio of two small integers. Such intervals have spacial names in music theory: octave (2:1), perfect fifth (3:2), perfect fourth (4:3), major third (5:4) and minor third (6/5). For example, if the root note has frequency , the major third will have frequency . These intervals can be played perfectly on some instruments (e.g. violin), or when singing.
Many modern musical instruments (e.g. piano, organ) are tuned in the "chromatic scale": an octave is divided into 12 equal intervals so that the ratio of the frequencies of the subsequent tones is . In such a tuning none of the harmonic intervals will be perfect. For example, the closest match to the frequency of the major third will be .
Let us characterize the "mismatch" between the harmonic interval and the chromatic interval by the ratio , where || is the absolute value and the logarithm is base 10. (For the major third this ratio will be .) Which one of the four intervals is the most "mismatched"?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here is a list of the chromatic and harmonic frequencies: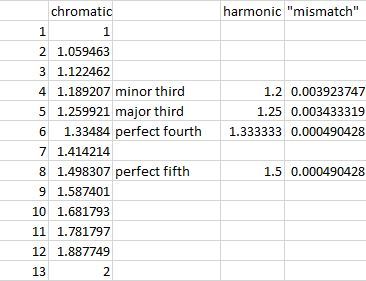 .. The minor third has the largest mismatch. Interestingly the fourth and the fifth has a pretty good match.
.. The minor third has the largest mismatch. Interestingly the fourth and the fifth has a pretty good match.