Perfect Polygons
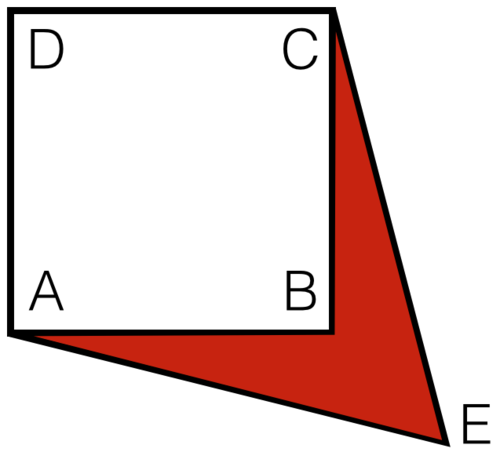 The diagram above shows a square
A
B
C
D
with diagonal
2
cm
long, and
A
E
C
is an equilateral triangle. Find the area of the quadrilateral
A
E
C
B
in
cm
2
.
The diagram above shows a square
A
B
C
D
with diagonal
2
cm
long, and
A
E
C
is an equilateral triangle. Find the area of the quadrilateral
A
E
C
B
in
cm
2
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
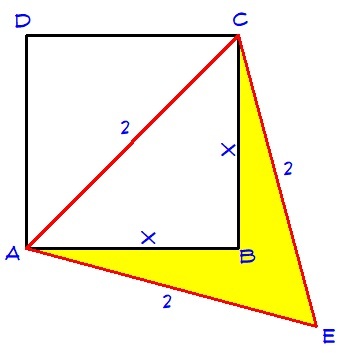 By pythagorean theorem, we have
By pythagorean theorem, we have
2 2 = x 2 + x 2 ⟹ x 2 = 2
The area of the quadrilateral A E C B is equal to the area of equilateral triangle C A E minus the area of triangle C A B . We have
A A E C B = 4 3 ( 2 2 ) − 2 1 ( 2 ) = 3 − 1
if the diagonals intersect at O
area of COB = 1/2
and area of COB =1/2 *SQR (3)
area of CBE = 1/2 *SQR (3) - 1/2
area of quadrilateral = 2 * ( 1/2 *SQR (3) - 1/2)
= SQR (3) - 1
Your COB are the same but the values are not.
The red area is the area of equilateral triangle A C E minus the area of right-triangle A B C .
△ A B C is a 4 5 ∘ − 4 5 ∘ − 9 0 ∘ right-triangle with hypotenuse of length 2 , so it has legs of length 2 2 . Thus, its area is 2 1 ⋅ 2 2 ⋅ 2 2 = 1 .
On the other hand, △ A C E has sides of length 2 , so its area is 4 2 2 3 = 3 .
Thus, the area of the shaded region is 3 − 1 .