Perfectly Squared Dice

Probability Level 2

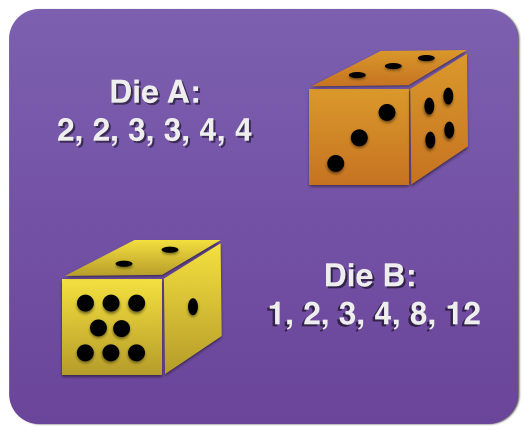Two strange six-sided dice are numbered on each side as follows:

Die A: 2, 2, 3, 3, 4, 4
Die B: 1, 2, 3, 4, 8, 12

If one were to roll these dice at the same time and multiply the two resulting values, what is the probability that the product would be a perfect square?

\frac{7}{36}

\frac{1}{3}

\frac{5}{18}

\frac{2}{3}

\frac{2}{9}

3 solutions

Chew-Seong Cheong
Aug 6, 2015

There are a total of $18$ outcomes of which $6$ outcomes are perfect squares (highlighted) as above. Therefore, the probability is $\frac{6}{18} = \boxed{\frac{1}{3}}$ .

Moderator note:

Good approach. For clarity, you should explain that each of these outcomes have an equal probability of occurring.

If dice A was 2, 2, 2, 3, 3, 4, how would the answer change?

Hadia Qadir
Aug 12, 2015

Total Permutations:36 Perfect Square happens at (Dice A, Dice B): (2,2),(2,2),(2,8),(2,8),(3,3),(3,3), (3,12),(3,12),(4,1),(4,1),(4,4),(4,4) or 12 total possibilities 12/36 = 1/3 or one third of the time.

Cleres Cupertino
Aug 6, 2015

$\begin{matrix} \sqrt { . } & 2 & 2 & 3 & 3 & 4 & 4 \\ 1 & \sqrt { 2 } & \sqrt { 2 } & \sqrt { 3 } & \sqrt { 3 } & 2 & 2 \\ 2 & 2 & 2 & \sqrt { 6 } & \sqrt { 6 } & 2\sqrt { 2 } & 2\sqrt { 2 } \\ 3 & \sqrt { 6 } & \sqrt { 6 } & 3 & 3 & 2\sqrt { 3 } & 2\sqrt { 3 } \\ 4 & 2\sqrt { 2 } & 2\sqrt { 2 } & 2\sqrt { 3 } & 2\sqrt { 3 } & 4 & 4 \\ 8 & 4 & 4 & 2\sqrt { 6 } & 2\sqrt { 6 } & 4\sqrt { 2 } & 2\sqrt { 2 } \\ 12 & 2\sqrt { 6 } & 2\sqrt { 6 } & 6 & 6 & 4\sqrt { 3 } & 4\sqrt { 3 } \end{matrix}$

$\large \frac{12}{36}=\frac{1}{3}$

Perfectly Squared Dice

3 solutions

Moderator note:

0 pending reports