Perimeter
In the polygon to the right, all adjacent edges are at right angles so that all its interior angles are either 9 0 ∘ or 2 7 0 ∘ .
The four longer edges are equal in length, and all of the shorter edges are also equal in length. The area of the shape is 528.
What is the perimeter?
The answer is 144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
It should be emphasized we don't have to tediously "count" the 33 squares. It suffices to note the center is 3 × 3 or 9 squares, and each of the four "arms" has 1 + 2 + 3 = 6 squares, giving a total count of 9 + 4 × 6 = 3 3 .
A similar idea works with perimeter. Counting just the vertical lines on the left side of the figure, there are 9 of them. Because of the 4-sided symmetry, this makes the perimeter 9 × 4 = 3 6 units.
Exactly the same method!!
Thank you for the nice solution. This is also how l have solved it.
This is exactly how I solved.
nicely solved!
I don't get it, in the way the problem is posed you have no way to know if
Long side = 3 x (short side)
Log in to reply
You didn't read it correctly. The problem mentions that the shorter edges are equal in length. Hence you can say that longer edge=3 x shorter edge.
Log in to reply
I read correctly, the problem is posed ambiguously.
Tomaž Cedilnik got it right bellow.
This problem borders between "Basic" and "Intermediate."
Relevant wiki: Composite Figures
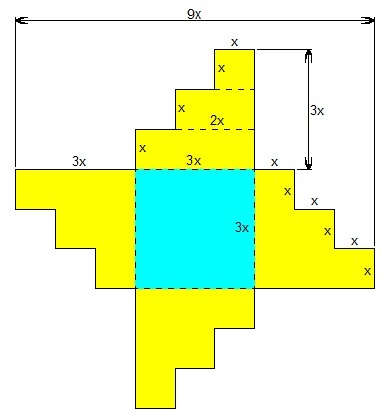 The area of the polygon is area of the yellow region plus area of the blue region. Since there are four yellow regions and one blue region, we have
The area of the polygon is area of the yellow region plus area of the blue region. Since there are four yellow regions and one blue region, we have
A = 4 [ x 2 + x ( 2 x ) + x ( 3 x ) ] + ( 3 x ) 2
5 2 8 = 4 ( x 2 + 2 x 2 + 3 x 2 ) + 9 x 2
5 2 8 = 2 4 x 2 + 9 x 2
5 2 8 = 3 3 x 2
x 2 = 1 6
x = 4
Therefore, the perimeter is
P = 4 ( 9 x ) = 4 ( 9 ) ( 4 ) = 1 4 4
Thank you. Nice illustrations and solution.
I don't see any guarantee that the long edges are exactly 3 times the short edges. As far as I can see they can be extended without affecting the short edges, by offsetting the opposing "arms".
Log in to reply
But it is given that the angles are right angles, right? So, trying to extend them will alter the angle.
The problem states not only that all the long edges are equal in length, but also that all the short edges are equal in length. If this is so, then it's impossible that the long edges are other than exactly 3x the short edges; lengthening the long edges would require lengthening one or more of the opposing short edges (the ones parallel to the long edges), rendering them unequal in length to the remaining short edges.
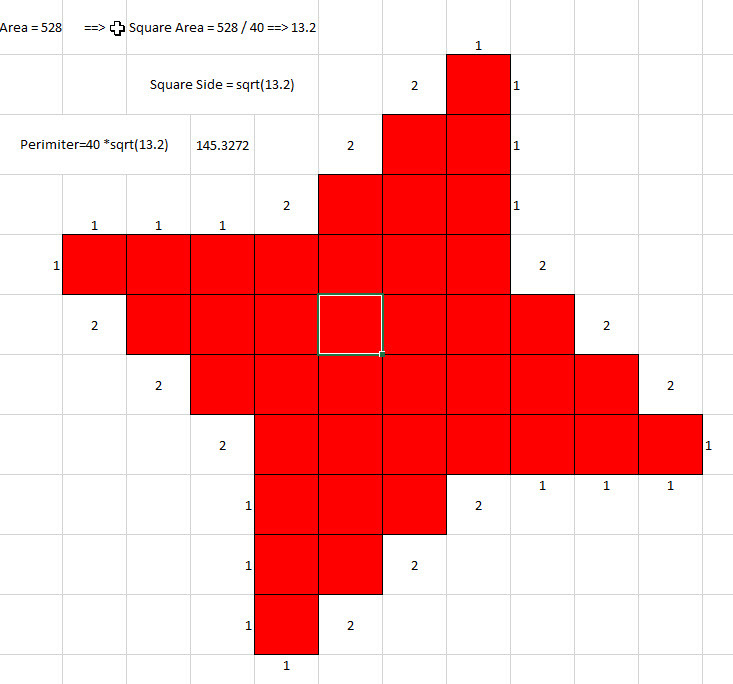
The perimeter can be anything from the interval (91.9, 145.3], and values from (128.7, 145.3) are reached in two cases each. The second interval can be extended to (112.6, 145.3) if we allow the "long" sides to be shorter than the "short" sides.
The obvious solution (and the only one where the sides line up as the picture suggests, making b=3a) is a=4, b=12, perimeter = 144. But its not stated anywhere that the sides do actually line up, and a perfectly acceptable solution is be, for example, a=2, b=12×sqrt(3), perimeter = 48(1+sqrt(3)), which is about 131.1. Jimmy Orioottis's example with picture illustrates the idea.
a has too be positive, but in the deformed case a=0 we get a square with side b = sqrt (528) = 4 sqrt (33), perimeter 16 sqrt (33) which is about 91.9.
As a grows, the perimeter grows and at a = sqrt (66/5) (about 3.63) it reaches maximum: b=4a and the perimeter is 40a, about 145.3.
As a grows further, the perimeter goes down. After just slight increase, a=4, we get the known solution of 144.
If we assume a<b (as they are referred to as short and long), the boundary case a = b = 4 sqrt (33) / 5 (about 4.60) takes the perimeter down to 28a = 112 sqrt (33) / 5, which is about 128.7.
Of course, we can increase a further, but then the "short" a will be longer than the "long" b. The perimeter goes down further. The deformed boundary case is b=0, which happens when a = sqrt (22) (about 4.69), then the perimeter is 24a = 24 sqrt (22), which is about 112.6.
How did youmget up there.
email to [email protected]
Why does everyone assume that 3 short sides = 1 long side.
The diagram implies it but the question does not mention that.
Using a ratio of 4 to 1, I get a different perimeter of 145.3272...
So the perimeter is a function of the ratio of short to long.
I looked at that, too. Short is a, long is b. Area is 24a^2 + b^2 = 528, perimeter is 24a + 4b.
Your case is, in fact, where perimeter reaches the largest possible value, see my answer.
They should have put more information in the description, instead of implying it in the diagram. Your layout doesn't visually match the diagram.
(a + 6b)^2 - 4 ((a + 2b) (3b)) + 4 (2b)^2 - 4 (b)^2 = 528
All we know is that a side comprised of one length a + 6 lengths b. Then you can start subtracting and adding regions which are defined in terms of a and b.
This reduces to: a^2 + 24*b^2 = 528
Therefore the integer solutions are: a = 12 and b = 4
The perimeter is: 4 (a + 6 b) = 144
However, to address your point, this also demonstrates that a = 3 b as 12 = 3 4.
We divide the figure and find we have three long bars each with 7 squares, that gives us 3 × 7 = 2 1 squares. The top and bottom each consists of one block of six so that gives us another 6 × 2 = 1 2 squares. Totally, there are 33 squares so each square has area 3 3 5 2 8 = 1 6 . Then the side of each square is 1 6 = 4 . It can also be seen that the perimeter of the figure is equivalent to that of a square of side 9 times one small square so the perimeter is 9 × 4 = 3 6 times the side of one small square which is 3 6 × 4 = 1 4 4 .
Thank you.
Please can you expatiate the part you got 36, that's the only part can't get figure out, thank you
Let shorter side be y ⟹ longer side is 3 y ⟹ 5 2 8 = 4 ( 3 y 2 + 2 y 2 + y 2 ) + 9 y 2 ⟹ 3 3 y 2 = 5 2 8 ⟹ y = 4 ⟹
longer side 3 y = 1 2 ⟹ Perimeter P = 4 ∗ ( 9 y ) = 4 ∗ ( 3 6 ) = 1 4 4
Relevant wiki: Challenging Composite Figures
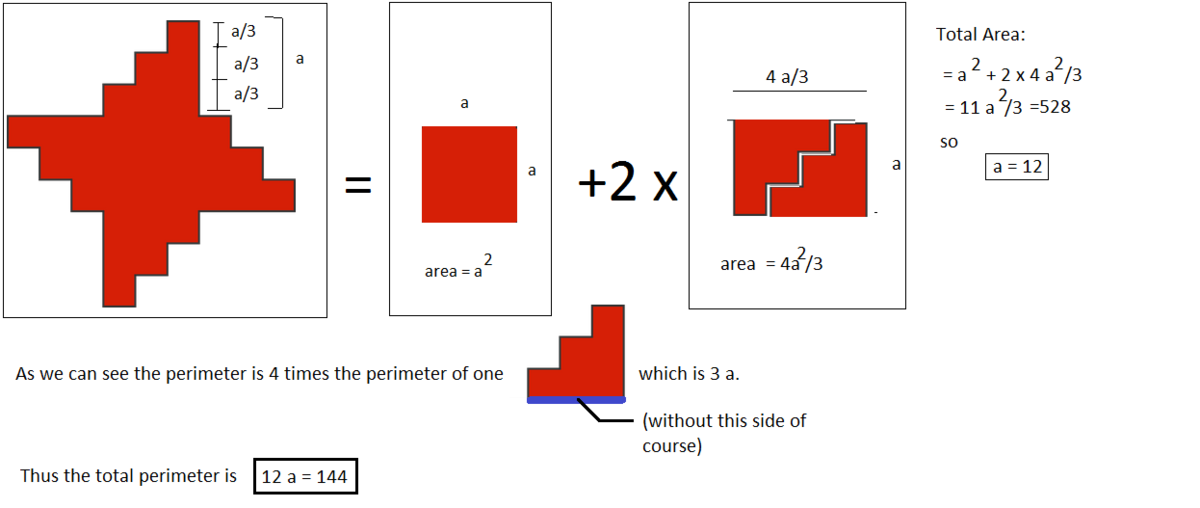
Divide the figures into small squares with side length a same length as the shorter edge as shown above.
We note that there are 33 (see notes) of these small squares making up the figure. Therefore, we have 3 3 a 2 = 5 2 8 , ⟹ a = 4 .
The perimeter is made up of 3 6 a = 3 6 × 4 = 1 4 4 (see notes).
Notes: