Perimeter Of Cross - General Form
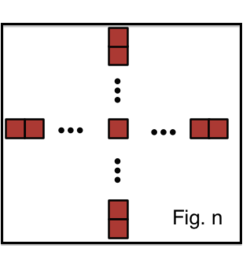In figure number
n
, where
n
represents the number of steps from
the initial state of the cross
, which of the following represents the perimeter?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The most common mistake made, is to not remember what the figures are.
Image
Note that figure 1 starts out as a single square, and it has no 'arm length'.
Log in to reply
Yes, when the figures have arm length, at that time the borderlines of the figure are the edges and the no. of line segments in the edges is the perimeter. Since, as squares are added at each of the ends of the previous figure, we can observe that the perimeter starts at 4 units in figure 1 and in each successive figure, we get a net gain of 8 units in perimeter. So, we can set up a function like this ---->
f ( x ) = 4 + 8 ( x − 1 ) = 4 + 8 x − 8 = 8 x − 4 where x = Figure no. and f ( x ) = Perimeter of figure x .
One more thing.... I think that this is more of an Algebra problem and not a Geometry problem as we can solve it using functions.
You should have explained how do you get the function f ( n ) = 8 n − 4 as for many people, the problem might not be simple as it is for you !!
If anyone has problems understanding this solution then refer to my solution posted below !!
why it is 8n-4 why not 8n+4
Log in to reply
It depends on how you take the value of n . Since, in the pictures of the problem, it is shown that the first figure having 4 units as perimeter is said as Fig. 1 and not Fig. 0, so the function is f ( n ) = 8 n − 4 .
If you consider the first figure as Fig. 0, then f ( n ) = 8 n + 4 is applicable !!
i think you have wrong answer because if we give the" n =0" ( one square ) we should find the perimeter = 4 not -4
Log in to reply
n can not be zero because n is fig. no. which started from 1. and at n=1 figure we get one square. not n=0.
yes, i also agree with you
I'm also having the same doubt. Question itself having the ambiguity,
Some people start numbering from 0,1,2,3,.....
And some can start from 1,2,3,....
So, i would like to say question is not in proper way, both answers ( 8n-4) and (8n+4) are correct, one option should be removed.
Log in to reply
Actually, if you look at the earlier questions of this set, you can see that the figure with perimeter 4 units, i.e., the first figure is marked as Figure 1 .
Now, if some dumb-asses don't know how to read or are blind, then what can the problem sharers do !!
P.S. -- Don't take this the wrong way. I am referring to others who are numbering from 0 as it is clearly specified in the picture that the numbering starts from 1 .
Observe that when we calculate the perimeter (no. of edges in the figure), we actually count the no. of line segments on the outline of the figure, i.e., the line segments in the border of the figure.
See that fig. 1 has perimeter of 4 units as it has 4 line segments in its border. Similarly, fig. 2 and 3 have perimeters 1 2 and 2 0 respectively.
So, each time a square is added to one end, the total perimeter increases by 2 units and since in each successive figure, there are 4 squares added (one to each end), so the total perimeter increases by 8 units and figure 1 has only perimeter of 4 units.
So, if we consider the figure no. as n , we can set up a function f to find the perimeter where f is defined as follows ->
f ( n ) = 4 + 8 ( n − 1 ) ⟹ f ( n ) = 4 + 8 n − 8 ⟹ f ( n ) = 8 n − 4
So, f ( n ) = 8 n − 4 where n = Figure no. and f ( n ) = Perimeter of figure n .
from the pattern we can see equation is 8n-4
simple Arithmetic Progression of 4, 12, 20, 28, 36 ...... so nth term will be 4 + (n-1)*8 = 4+8n-8 = 8n-4
It is simple.it is just the equation 8n-4.