Perimeter Patterns

When a new box is added at one of the "ends" of figure 2, it adds exactly 2 new edges:

Since 4 boxes are added, the perimeter change is +8, so $12+8=20.$

Number of boxes 'n' P=2n+2

We can simply count the each side of a square which faces the outer side, and find 20 of them:

Focus on the ratio here. For one square the perimeter was 4. For another 4 squares the perimeter raised to 12. So, the perimeter raises 8 units for 4 square. So, the perimeter of fig. 3 will be 12 + 8 units=20 units.

The perimeter is 2(n + 1), where n is the number of squares present.

By counting all the outer sides of the figure, taking 1 side=1 unit, we get its perimeter as 20.

$Fig.1:P=4\Longrightarrow (4\cdot 1)$

$Fig.2:P=12\Longrightarrow (4\cdot 3)$

$Fig.3:P=4\Longrightarrow (4\cdot 5)$

$\vdots$

Having noticed this:

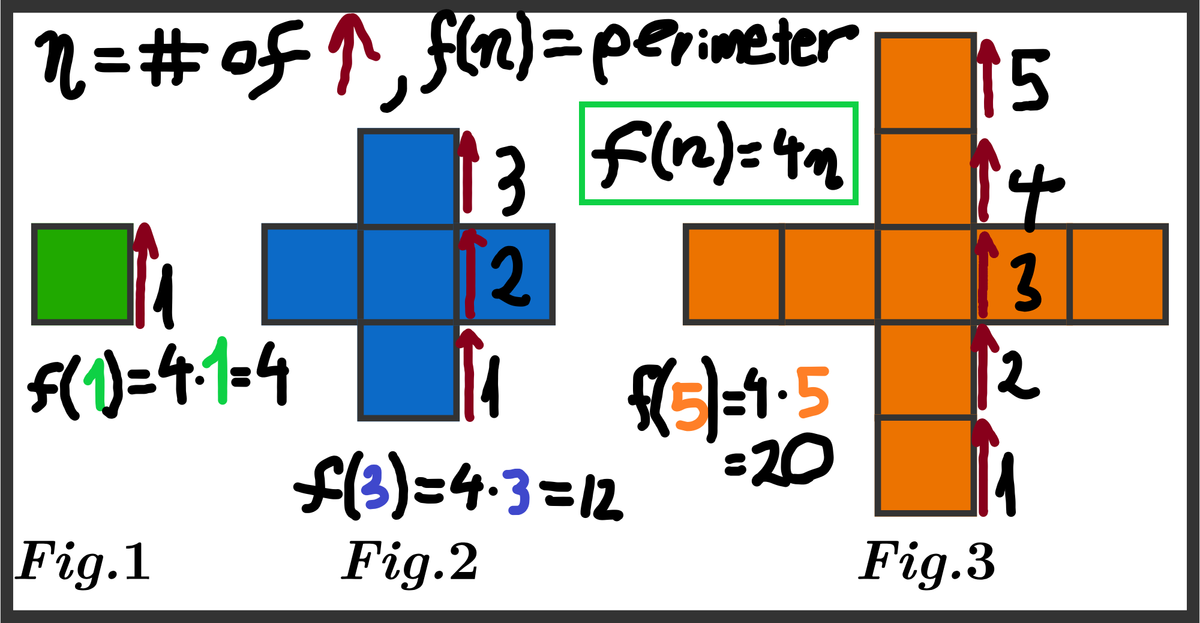
$n=number$ $of$ $arrows,$ $f(n)=perimeter$

Then:

$\boxed{f(n)=4n}$

The simple way to do this is simply counting the edges

perimeter figure 1 = 1*4

figure 2 = 3*4

figure 3 = 5*4

y = (2x-1)4

or you could just count the number of edges sticking out on one of them sticks and times it by 4. 1 4 3 4 5*4

4 sides with 5 units each. 4 x 5 = 20

4 boxes have 3 sides, and 4 have 2 sides. Therefore (3 x 4) + (2 x 4) = 20

We can find the solution with this formula P=n.4-(n-1).2

For figure n, it simplifies down to $p(n)=4*(2n-1)$ . Here, the value is simply $p(3)=4*(2(3)-1)$ , which is 20.

In fig. 1 the unit of edge is 4unit and the fig.2 the unit of edge is 8unit.. It means that when the blocks are increased the no. Will also be increased. It increases by multiple of 4 b/w the 2 gaping..ex.4×3=12,4×5=20 so total block of perimeter is 4 +8+8=20 i.e p= 2n+2

Since the first figure has 4 units, the second one has12 units, this means that they were getting the perimeter of the figures and this meant that one side of the square has 1 unit. If you count the sides in figure 3 you will be able to find out that they are 20 which means you don't count those that are attached on the sides.Marion Edith from Mpesa foundation academy.

   AT LAST  YOU GET YOUR ANSWER AS=20

Find the length from 1 end to other and multiply into 4

Every time a box is added it increases the length of each arm by one unit or the perimeter increases by 2 units. For four boxes it increases by 8 units and so the answer is 12+8=20.

4,12,20

Each side block is of 5 units ,so four sides will have 20 Ans

every time there will be increment of 8 units (3*4-4)

Take Fig. 1. The Square is having 4-Sides and each side is 1-Unit in length and so the Periphery of square is 4-Units. In big Cross, 9 Squares are included so the total Periphery of 9 squares will be 36 Units. But in the Fig. 3, there are 16 Sides of 9 squares which are not Part of Periphery, so 36 - 16 = 20 sides, which are making the Periphery of Fig. 3. Thus Periphery will be 20 Units.

It is given that the square one has a perimeter of 4 units.This means that each side of the square measures 1 unit.So in the last figure we just have to count the number of edges of each square.