Perimeter Of Cross - What's Next?
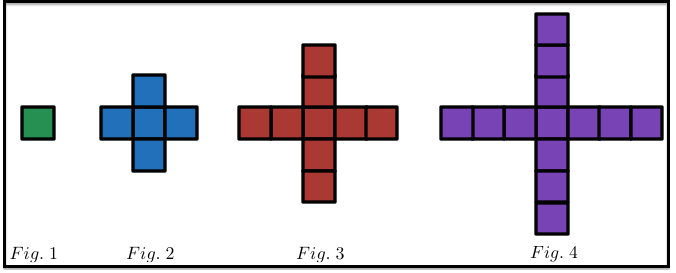 What is the perimeter of figure 5 (not shown)?
What is the perimeter of figure 5 (not shown)?
This problem is part of Arron's set The Cross Investigations - Perimeter .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
There is an increment of 8 from previous cross to next.
4+(n-1)8 where n=number of sides
how do you derive this from
P=2n+2
the perimeter is the number of the outline edges. in Fig.1 let's name it "level 1 box" . in Fig.2, boxes level 2 added to box level 1. so,the 2 joint edges for every box is out of the of perimeter. consequently, the perimeter increases by 3 edges and decreases by 2 edges for every box added. and by the fact that for each figure we add 4 boxes so, the number of boxes added in every figure N = 4 ( x - 1 ) , x for figure no.
hence, the perimeter is equal to the edges of every box added to level 1 box - the joint edges + the 4 top edges
perimeter = 4N - 2N (joint edges) + 4 (top edges) .. simplify, perimeter = 2 ( N + 2 ) as N is the number of the whole added boxes N = 4 ( x - 1 ) so, the function is:
f ( x ) = 2 ( N + 2 )
in figure 5. N = 4 ( 5 -1 ) = 16 boxes f ( x ) = 2 ( 1 6 + 2 ) = 3 6
The increment shall always be 2 for each side. The start of it 3 on each side. Hence next will be 5,7,9. 9 x4 = 36
For fig.1 perimeter=4 (4 1=4), For fig.2 perimeter=12 (4 3=12), For fig.3 perimeter=20 (4 5=20), For fig.4 perimeter=28 (4 7=28), Hence For fig.5 perimeter=36 (4*9=36)
This question can be solved by applying the Arithmetic Progressions(A.P.). As we know, the perimeter for the first, second and third figures is 4, 12 and 20 respectively. From here, we know that the first term, a=4. The common difference, d= 12-4=8. In order to find the perimeter of the fifth term(let the n in this case be 5), we apply the formula a+(n-1)d=4+(5-1)(8)=36.
It is quite simple.One side of each square is equal to 1 unit.So we have to just count the sides of square in the figure.
Observe that when we calculate the perimeter (no. of edges in the figure), we actually count the no. of line segments on the outline of the figure, i.e., the line segments in the border of the figure.
See that fig. 1 has perimeter of 4 units as it has 4 line segments in its border. Similarly, fig. 2 and 3 have perimeters 1 2 and 2 0 respectively.
So, each time a square is added to one end, the total perimeter increases by 2 units and since in each successive figure, there are 4 squares added (one to each end), so the total perimeter increases by 8 units.
So, if we consider the figure no. as x , we can set up a function as f ( x ) = 4 + 8 ( x − 1 ) where f ( x ) is the perimeter of the figure.
Putting x = 5 , we get f ( x ) = 4 + 8 × ( 5 − 1 ) = 4 + 3 2 = 3 6