Perimeter of the First
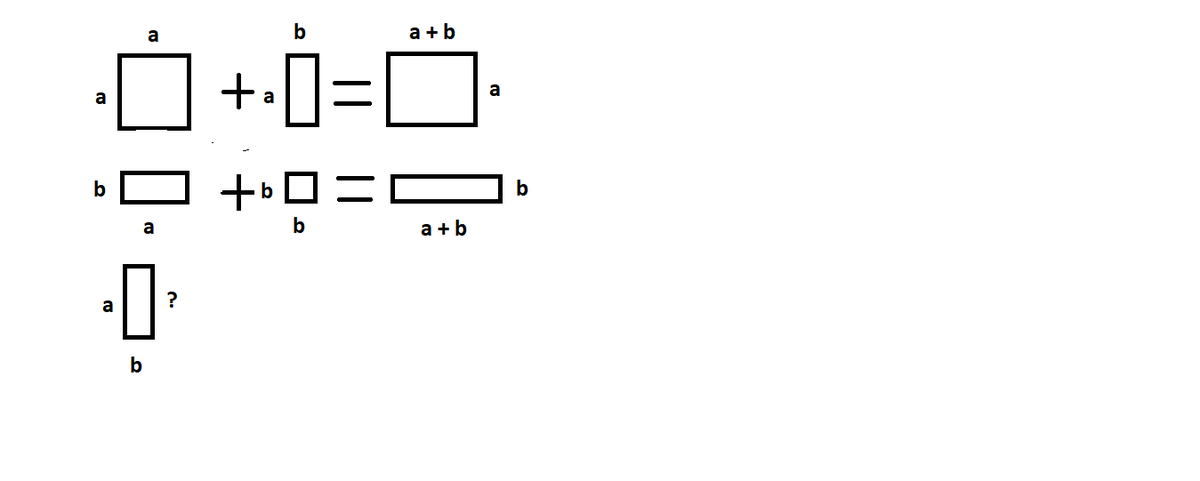
A square combine with a first rectangle which the long side of it equals to the side of a square to make a second rectangle which its perimeter equal to 26.The first rectangle combine with a square which side of it equals to the short side of the first rectangle to make a third rectangle which its perimeter is 22.Find the perimeter of the first rectangle.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Perimeter of the second rectangle formula: 2 ( a + b + a ) = 2 ( 2 a + b ) = 4 a + 2 b = 2 6 ⟹ 2 a + b = 1 3
Perimeter of the third rectangle formula: 2 ( a + b + b ) = 2 ( a + 2 b ) = 4 b + 2 a = 2 2
2 a − 2 a + + 4 b b 3 b = = = 2 2 1 3 9
3 b = 9 ⟹ b = 3
2 a + 3 = 1 3 ⟹ 2 a = 1 0 ⟹ a = 5
2 ( 3 + 5 ) = 2 × 8 = 1 6
Relevant wiki: Similar Polygons - Area and Perimeter Relations
The second rectangle would have a perimeter of 2 × ( a + b + a ) = 2 a + 2 a + 2 b = 4 a + 2 b
and we know that 4 a + 2 b = 2 6 as stated in the question.
The third rectangle would have a perimeter of 2 × ( a + b + b ) = 2 a + 2 b + 2 b = 2 a + 4 b
Adding both equations up we have 6 a + 6 b = 2 6 + 2 2 ⟹ 4 8 dividing both sides by 3 and we have 2 a + 2 b = 1 6