Perimeter of the triangle
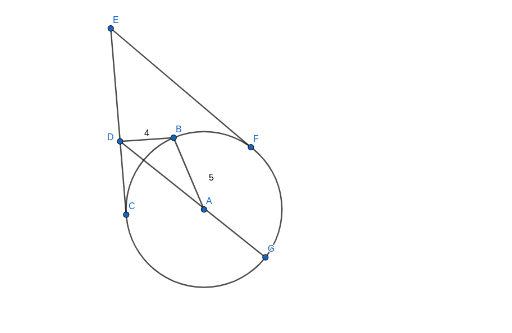
The figure above shows a circle with as its center and has a radius of 5.
and are both tangent to the circle, and is a secant line that passes through and intersects with the circle at .
, and .
Find the perimeter of .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Connect A C and draw a perpendicular line from B down to A C and let the intersection be point I . Because both ∠ E D B and ∠ D C A are 9 0 ∘ , B I would be parallel and equal to D C , C I would also be perpendicular and equal to D B , therefore A I = 5 − 4 = 1 , and ∠ B I A = 9 0 ∘ .
According to the Pythagorean theorem:
D C = B I = 5 2 − 1 2 = 2 4 .
Then, according to the Tangent-secant theorem:
D C 2 = D H × D G .
Let D H = x
x ( 1 0 + x ) = 2 4
x 2 + 1 0 x − 2 4 = 0
( x + 1 2 ) ( x − 2 ) = 0
x = − 1 2 or 2 , 2 being the only valid answer here.
Therefore, P △ D B A = 2 + 5 + 4 + 5 = 1 6