Perimeter=1
The
pentagon's perimeter is
. Each of the
sides is equal to
and
.
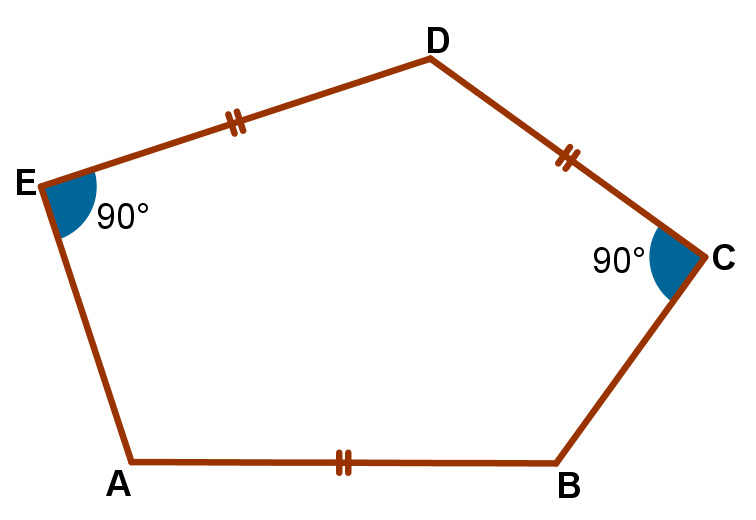
What is the area of the pentagon?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Drawing altitude D F and few more lines, we form the symmetries about A D and D B in the diagram, which show that
Since the perimeter of the whole polygon is 4 , then ∣ A B ∣ + ∣ C D ∣ + ∣ D E ∣ + ( ∣ E A ∣ + ∣ A F ∣ ) ∣ A B ∣ + ∣ A B ∣ + ∣ A B ∣ + ∣ A B ∣ ∣ A B ∣ = 4 = 4 = 1 Definition of perimeter. Using the previous info
Thus, since the pentagon can visually be presented as the square of side length 1 (by flipping Δ D E A and Δ D B C ), the area of the given polygon is 1 .