Perimeters !
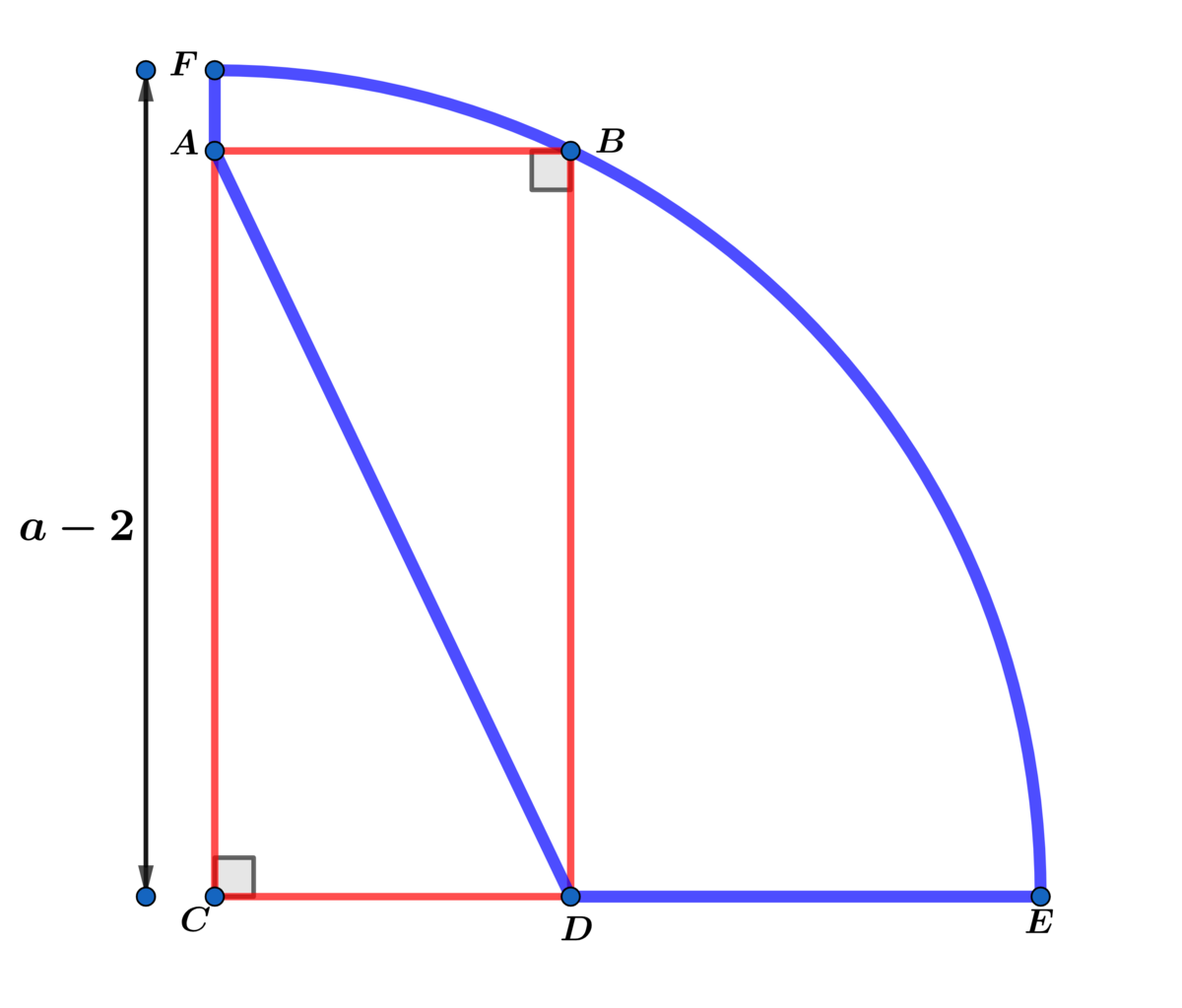
In the diagram above is an inscribed rectangle with diagonal ,
where , and the radius of quarter circle is .
Find the value of for which the perimeter(outlined in blue) above is .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The diagonals of a rectangle are congruent ⟹ in rectangle A B D C we have A D = r = a − 2
x + y = a ⟹ y = a − x ⟹ x 2 + ( a − x ) 2 = ( a − 2 ) 2 ⟹
2 x 2 − 2 a x + 4 ( a − 1 ) = 0 ⟹ x = 2 a ± a 2 − 8 a + 8
( x = 2 a − a 2 − 8 a + 8 ⟹ y = 2 a + a 2 − 8 a + 8 )
and
( x = 2 a + a 2 − 8 a + 8 ⟹ y = 2 a − a 2 − 8 a + 8 )
For either pair ( x , y ) we obtain the same perimeter since the square root part will cancel out
so choosing ( x = 2 a − a 2 − 8 a + 8 , y = 2 a + a 2 − 8 a + 8 )
⟹ The Perimeter P = ( a − 2 ) + [ ( a − 2 ) − 2 1 ( a − a 2 − 8 a + 8 ) ] +
[ ( a − 2 ) − 2 1 ( a + a 2 − 8 a + 8 ) ] + 2 π ( a − 2 ) =
2 a − 6 + 2 π ( a − 2 ) = 2 ( 4 + π ) a − 1 2 − 2 π = 1 0 + 3 π ⟹
( 4 + π ) a = 3 2 + 8 π = 8 ( 4 + π ) ⟹ a = 8 .