Perimeters and Areas!
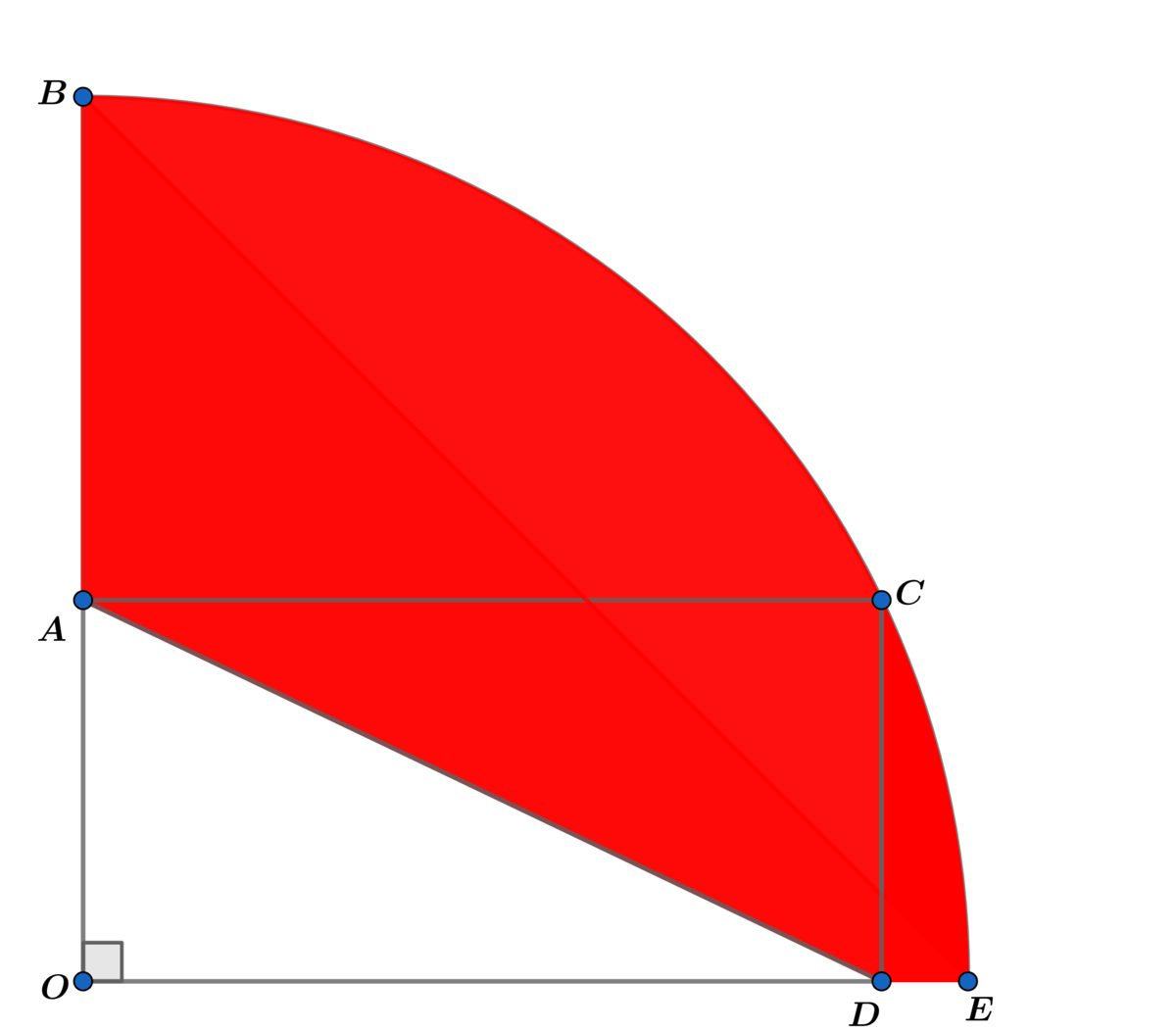
If the area of red shaded region is 9 π − 7 and the sum of the length and the width of rectangle O A C D is r + 2 , where r is the radius of the quarter circle, and the perimeter P of the shaded region can be expressed as P = α + β π , where α and β are coprime positive integers, find α + β .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Chew-Seong Cheong - Hi! It's an easy way to locate the value of r (I used it too), but how do we know that 2 a b is rational?
Log in to reply
You are right, we don't know. I just have to assume it first.
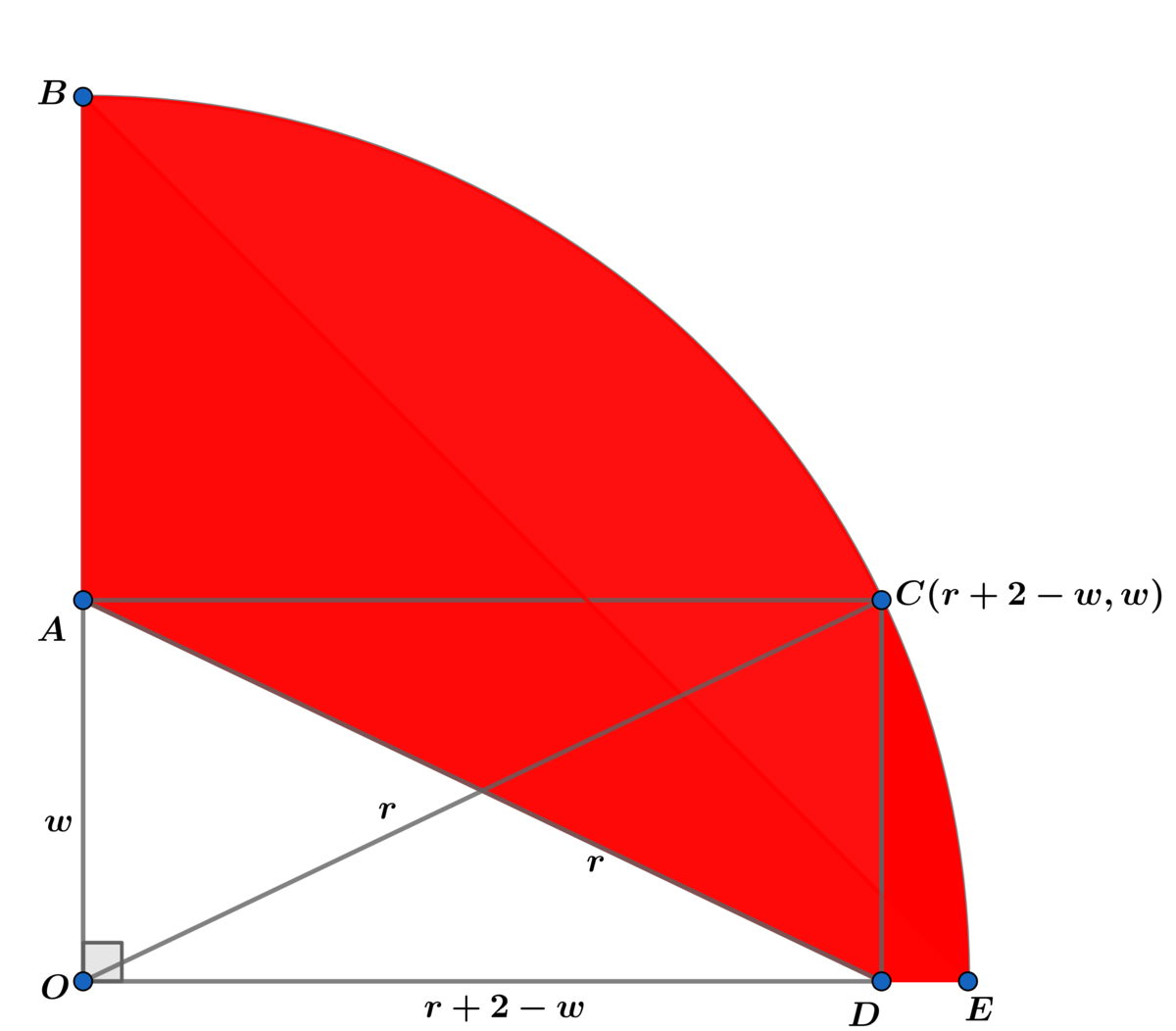
The diagonals of rectangle O A C D are congruent ⟹ A D ≅ O C = r ⟹
P = r + ( r − w ) + r − ( r + 2 − w ) + 2 π r = 2 ( 4 + π ) r − 4
Using point C above we have: ( r + 2 − w ) 2 + w 2 = r 2 ⟹
2 w 2 − 2 ( r + 2 ) w + 4 ( r + 1 ) = 0 ⟹ w 2 − ( r + 2 ) w + 2 ( r + 1 ) = 0 ⟹
w = 2 r + 2 ± ( r − 2 ) 2 − 8
Let A R be the red shaded region.
Using either value of w ⟹
A R = 4 1 ( π r 2 − 2 1 ( r + 2 − ( r − 2 ) 2 − 8 ) ( r + 2 + ( r − 2 ) 2 − 8 ) ) =
4 1 ( π r 2 − 2 1 ( ( r + 2 ) 2 − ( ( r − 2 ) 2 − 8 ) ) ) = 4 1 ( π r 2 − 4 r − 4 ) = 9 π − 7
⟹ π r 2 − 4 r + 1 2 ( 2 − 3 π ) = 0 ⟹ r = π 2 ( 1 ± ( 3 π − 1 ) ) dropping negative root
⟹ r = 6 ⟹ P = 2 2 0 + 6 π = 1 0 + 3 π = α + β π ⟹ α + β = 1 3 .
Let
O
D
=
A
C
=
x
and
O
A
=
C
D
=
y
.
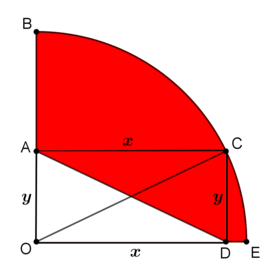 First it is given that
x
+
y
=
r
+
2
By Pythagoras’s theorem on right
△
O
A
C
,
First it is given that
x
+
y
=
r
+
2
By Pythagoras’s theorem on right
△
O
A
C
,
A C 2 + O A 2 = O C 2 ⇒ x 2 + y 2 = r 2 ⇔ ( x + y ) 2 − 2 x y − r 2 = 0 ⇔ ( r + 2 ) 2 − 2 x y − r 2 = 0 ⇔ 4 r + 4 − 2 x y = 0 ( 1 ) Moreover, for the area of the red region we have
[ A B C E D ] = [ O B C E ] − [ O A D ] ⇒ 9 π − 7 = 4 1 π r 2 − 2 1 x y ⇔ 2 x y = π r 2 − 3 6 π + 2 8 ( 2 ) Combining ( 1 ) and ( 2 ) , we have an equation for r :
4 r + 4 − π r 2 + 3 6 π − 2 8 = 0 ⇔ π r 2 − 4 r + 2 4 − 3 6 π = 0 ⇔ r > 0 r = 6 For the perimeter,
P = A B + B C D + E D + A D = ( r − y ) + 4 1 2 π r + ( r − x ) + r = 3 r − ( x + y ) + 2 π r = 3 r − ( r + 2 ) + 2 π r = r = 6 1 0 + 3 π For the answer, α = 1 0 , β = 3 , thus, α + β = 1 3 .
Let A O = a and O D = b . Then the area of the red region is 4 π r 2 − 2 a b = 9 π − 7 . Assuming that 4 π r 2 = 9 π ⟹ r = 6 and 2 a b = 7 ⟹ a b = 1 4 . Given that a + b = r + 2 = 8 ⟹ b = 8 − a . Then
a b a ( 8 − a ) a 2 − 8 a + 1 4 ⟹ a = 1 4 = 1 4 = 0 = 2 8 ± 8 2 − 4 ⋅ 1 4 = 4 ± 2
Assuming b > a , then a = 4 − 2 and b = 4 + 2 . Then the perimeter of the red region:
P = A B + A D + D E + B C E a r c = r − a + a 2 + b 2 + r − b + 4 2 π r = 2 + 2 + 6 + 2 − 2 + 3 π = 1 0 + 3 π
Therefore α + β = 1 0 + 3 = 1 3 .