Period of Small Oscillations

Classical Mechanics Level 3

Mass of Planck is m m and that of the solid cylinder is 8 m 8m . Springs are light. The planck are slightly displaced from equilibrium and then released.
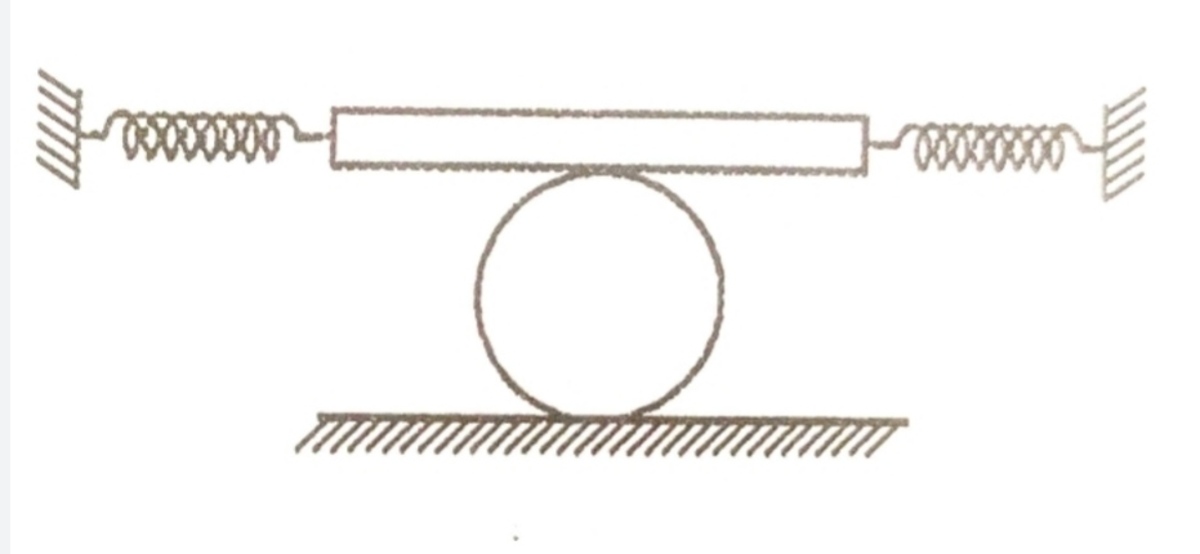
Find the period of small oscillations ( in seconds ) of the planck.
There is no slipping at any contact point .
The ratio of the the mass of the planck and stiffness of the spring is m k = 2 π 2 \frac{m}{k}=\frac{2}{π^{2}}


The answer is 4.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The linear velocity of the plank is related to the angular velocity of the cylinder as

v = 2 R ω v=2R\omega , where R R is the radius of the cylinder.

Total mechanical energy of the system is

2 × 1 2 k x 2 + 1 2 m v 2 + 2\times \dfrac 12 kx^2+\dfrac 12 mv^2+

1 2 ( 1 2 × 8 m R 2 + 8 m R 2 ) ω 2 \dfrac 12 (\frac 12 \times 8mR^2+8mR^2)\omega^2

= k x 2 + 2 m v 2 =kx^2+2mv^2

Where x x is the displacement of the plank. Since this energy remains conserved, we have

k x v + 2 m v d v d t = 0 kxv+2mv\dfrac{dv}{dt}=0

⟹ d v d t = − k 2 m x = − π 2 4 x \implies \dfrac {dv}{dt}=-\dfrac {k}{2m}x=-\dfrac {π^2}{4}x

Hence the period of motion of the system is

T = 2 π 4 π 2 = 4 T=2π\sqrt {\dfrac {4}{π^2}}=\boxed 4 units.

2 Helpful 2 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...