Periodic
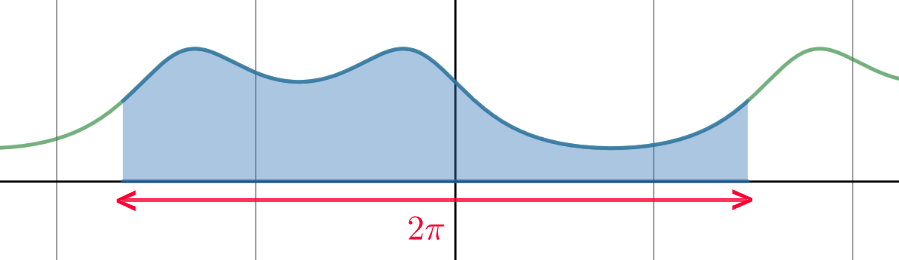
There is always a constant area A above a line segment (of length 2 π lying on the x-axis) and under the curve sin 2 x + sin x + 1 1 ,which equals A = q p q + p q π for coprime integers p and q .
- Does this mean there is always a constant length L of the curve sin 2 x + sin x + 1 1 above a line segment (of length 2 π lying on the x-axis)?
Find p + q and add 1 to your answer if you think the above statement is correct, otherwise add 0
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There's an error in the second last step
= i 3 1 × 2 i I m ( ∫ 0 2 π sin x − x d x )
Isn't it supposed to be ∫ 0 2 π sin x − ω d x ?
If ω = − 2 1 + 2 1 i 3 is a primitive cube root of unity, then ∫ 0 2 π sin x − ω d x = ∫ ∣ z ∣ = 1 i z [ ( 2 i z − z − 1 ) − ω ] d z = 2 ∫ ∣ z ∣ = 1 z 2 − 2 i ω z − 1 d z = 2 ∫ ∣ z ∣ = 1 ( z − α + ) ( z − α − ) d z = 4 π i R e s z = α + ( z − α + ) ( z − α − ) 1 = α + − α − 4 π i where α ± = i ω ± 1 − ω 2 = 2 ± 3 + 2 3 − 3 + i 2 ± 2 3 − 3 − 1 noting that ∣ α + ∣ < 1 < ∣ α − ∣ . Thus ∫ 0 2 π sin x − ω d x = 3 + 2 3 + i 2 3 − 3 4 π i = 3 π i [ 3 + 2 3 − i 2 3 − 3 ] Thus ∫ 0 2 π sin 2 x + sin x + 1 d x = ∫ 0 2 π ( sin x − ω ) ( sin x − ω 2 ) d x = ω − ω 2 1 ∫ 0 2 π ( sin x − ω 1 − sin x − ω 2 1 ) = i 3 1 × 2 i I m ( ∫ 0 2 π sin x − ω d x ) = 3 2 × 3 π 3 + 2 3 = 3 2 π 3 + 2 3 so that p = 2 and q = 3 .
Since the arc-length is the integral of g ( x ) = 1 + f ′ ( x ) 2 with respect to x , where f ( x ) = sin 2 x + sin x + 1 1 is a periodic function of x of period 2 π , the function g ( x ) is also periodic of period 2 π , and hence the arc-length over an interval of length 2 π is independent of that interval's position. This makes the answer 2 + 3 + 1 = 6 .