Perpendicular chords in circle
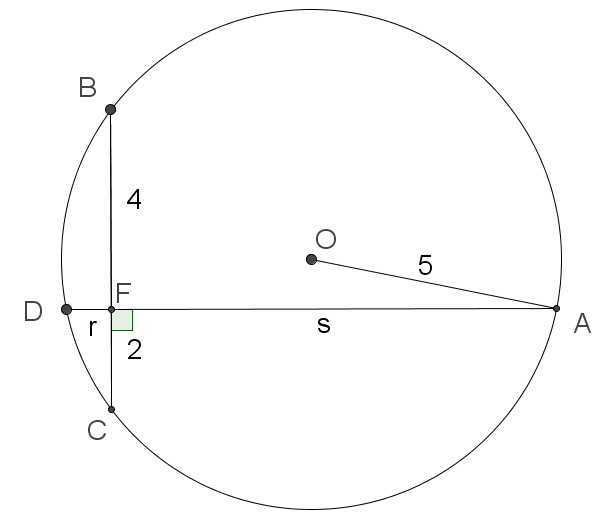
Find the value of ⌈ 1 0 0 ( r + s ) ⌉ .
The answer is 980.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Elegant! I love this solution. Thank for sharing.
Nice Solution.
Exactly Same Way.
Same approach.
Exactly the same way.
Jon, I hate to be picayune, but the problem asks for the ceiling function of 100(r + s), which is the ceiling function of 400*sqrt(6) = 980.
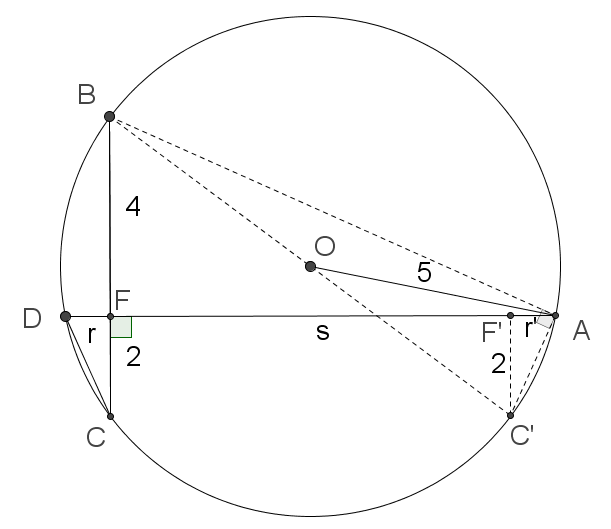
Construct the right angled triangle A F ′ C ′ , such that A F ′ = D F = r and C ′ F ′ = C F = 2 , as shown.
Note that ∠ B A C ′ = 9 0 ∘ (as ∠ B A D = ∠ B C D and ∠ D A C ′ = ∠ A D C ). This means that B C ′ is a diameter. Now B C ′ 2 = A C ′ 2 + A B 2 = ( r 2 + 2 2 ) + ( 4 2 + s 2 ) , which means that r 2 + s 2 = 8 0 (as B C ′ = 2 O A = 1 0 ). On the other hand, it is clear that △ F D C is similar to △ F B A , which means that r s = 4 ( 2 ) = 8 . Thus r + s = ( r 2 + s 2 ) + 2 r s = 8 0 + 1 6 = 9 6 = 9 . 7 9 7 9 6 and hence ⌈ 1 0 0 ( r + s ) ⌉ = 9 8 0 .
Arrggh.. Got 2answer wrong then finally got right one but typed 979. You should to tell to round up to nearest integer
Log in to reply
The notation given in the problem clearly asks for the ceiling function, not the floor function; don't feel bad, very easy to get confused. It would have been better to give the answer as 4*sqrt(6).
Novel approach. Could not think of it !! Congratulations. Up voted.
Let M and N be the projections of O onto A D and B C , respectively. Then M is the midpoint of A D and N is the midpoint of B C . Then B N = C N = 3 , so N F = 1 . Since O M F N is a rectangle, O M = 1 . Then by Pythagoras on right triangle O M A , A M = 2 6 . Also, A M is half of A D = r + s , so r + s = 4 6 .