Perpendicular distance between two parallel lines

Consider two lines $\;l_1: 2x+3y+1=0$ and $\;l_2: 2x+3y+5=0$ that are parallel to each other. Observe that the point $A(-1,-1)$ lies on line $l_2$ since it it satisfies the equation of the line.

The perpendicular distance between $l_1$ and $l_2$ is the distance between point $A$ and line $l_1$ . $\begin{aligned} d&=\frac{\mid 2\cdot (-1)+3\cdot (-1)+1 \mid}{\sqrt{2^2+3^2}} \\ &=\frac{4}{\sqrt{13}} \end{aligned}$ Therefore, the perpendicular distance between the lines $2x+3y+1=0$ and $2x+3y+5=0$ is $\boxed{\frac{4}{\sqrt{13}}}$

Both lines have a slope of $-\cfrac{2}{3}$ , but the first line has a $y$ -intercept of $-\cfrac{1}{3}$ and the second line has a $y$ -intercept of $-\cfrac{5}{3}$ .

Draw $\triangle ABC$ as follows:

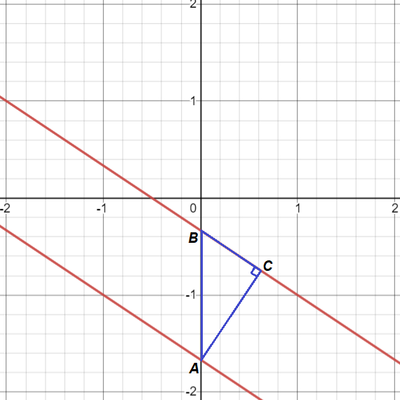
Since the two $y$ -intercepts are $-\cfrac{1}{3}$ and $-\cfrac{5}{3}$ , $AB = -\cfrac{1}{3} - -\cfrac{5}{3} = \cfrac{4}{3}$ .

Since both lines have a slope of $-\cfrac{2}{3}$ , the ratio of $BC$ to $AC$ will be $2:3$ , so let $BC = 2k$ and $AC = 3k$ .

By the Pythagorean Theorem, $(2k)^2 + (3k)^2 = \bigg(\cfrac{4}{3}\bigg)^2$ , which solves to $k = \cfrac{4}{3\sqrt{13}}$ .

The perpendicular distance is then $AC = 3k = \boxed{\cfrac{4}{\sqrt{13}}}$ .