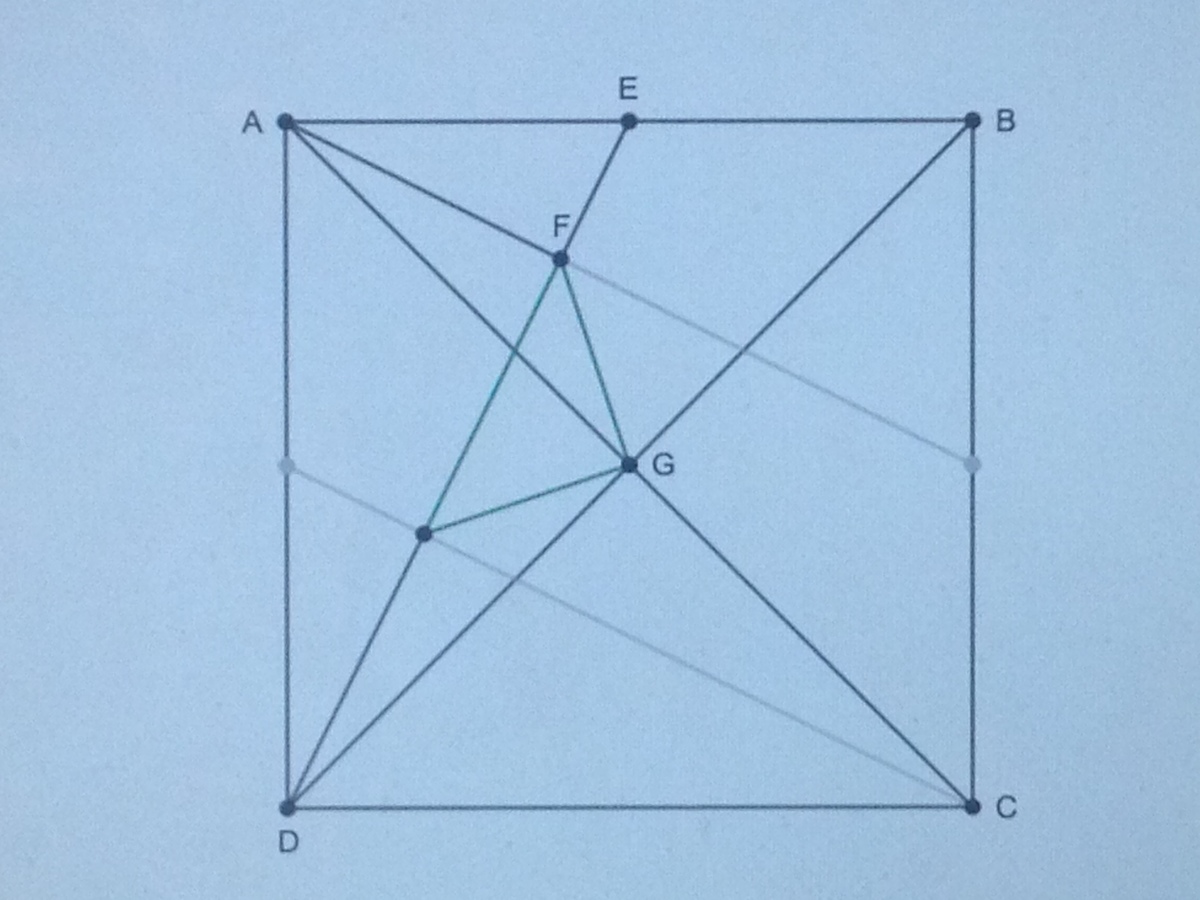
Perpendicular midpoint angle inside a square
Consider the square ABCD. On line AB, mark the point E such that AE=EB. Draw line DE. On line DE, mark the point F such that AF is perpendicular to DE. Draw line AF. Draw lines AC and BD and mark their point of intersection G. Draw line FG. What is the angle DFG?
In this picture, the angles AFE=AFD=AGB=AGD=BGC=CGD=90 degrees. So what is the angle DFG?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since AF is perpendicular do DE, if we extend the line AF until it touches BC we find that it intersects line BC exactly halfway in-between point B and C. This means line AF is actually just line DE rotated 90 degrees and put in the appropriate corner (as well as shrunk), which should allow us to create a similar line from point C that is perpendicular to line DE. Drawing a line from their point of intersection to point G creates a line that is of equal length of line FG. These two lines form along with a segment of line DE an isosceles right triangle (green lines in image below) since the shorter lines were constructed in the exact same way just rotated 90 degrees from each other. Since the sum of the angles in a triangle is 180 degrees, one angle is 90 degrees and the other two are the same, they must be 45 degrees, and thus the angle DFG is 45 degrees.