Perplexing Pizza Crust
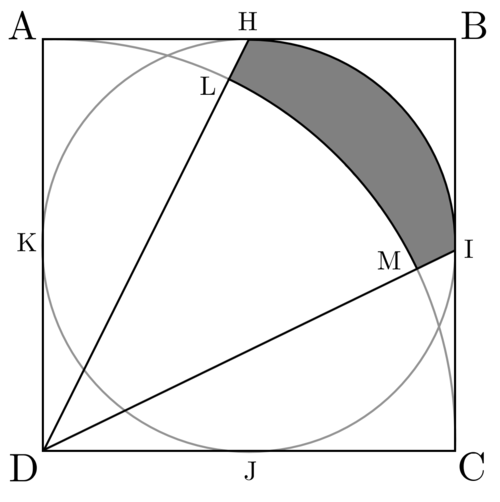A square box
A
B
C
D
of side length
1
0
0
contains a slice of pizza. The box meets with an inscribed circle at points of tangency
H
,
I
,
J
,
K
, and there is an inscribed circle quadrant with centre
D
.
Let L be the point where arc A C intersects the line D H , and M be the point where the same arc intersects the line D I . Find the area of the pizza crust (the shaded region H I M L ) to the nearest integer.
Details and Assumptions :
-
Use the approximation tan − 1 ( 2 1 ) = 0 . 4 6 4 .
-
Use the approximation π = 3 . 1 4 2 .
Created by Michael Fuller . Popular geometry problems: "Star Stumper" , "Not your average shuriken"
The answer is 1249.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Slightly different approach.
D
I
=
1
0
0
2
+
5
0
2
=
5
0
5
.
∠
H
D
I
=
2
3
.
1
4
2
−
2
∗
0
.
4
6
2
=
.
6
4
3
.
R
e
q
u
i
r
e
d
a
r
e
a
=
Δ
H
I
D
−
S
e
c
t
o
r
L
M
D
+
S
e
g
m
e
n
t
5
0
H
I
.
R
e
q
u
i
r
e
d
a
r
e
a
=
2
5
∗
5
0
2
S
i
n
0
.
6
4
3
−
2
1
0
0
2
∗
6
4
3
+
{
2
5
0
2
∗
(
2
3
.
1
4
2
−
S
i
n
2
3
.
1
4
2
)
}
=
1
2
4
6
.
I made a mistake in LMD,had taken 50 in place of 100.
I took values given in the problem.
Log in to reply
That's a great method. :) I think that the reason you ended up with 1 2 4 6 rather than 1 2 4 9 is because of the sin ( 0 . 6 4 3 ) factor. On the one hand, sin ( 0 . 6 4 3 ) = 0 . 5 9 9 5 9 9 0 3 8 . . . . . But if sin ( ∠ H D I ) is calculated before substituting the given value for tan − 1 ( 2 1 ) then we would have
sin ( ∠ H D I ) = sin ( 2 π − 2 tan − 1 ( 2 1 ) ) = cos ( 2 tan − 1 ( 2 1 ) ) =
2 cos 2 ( tan − 1 ( 2 1 ) ) − 1 = 2 cos 2 ( cos − 1 ( 5 2 ) ) − 1 = 2 ∗ ( 5 2 ) 2 − 1 = 5 8 − 1 = 5 3 = 0 . 6 .
When sin ( 0 . 6 4 3 ) is replaced by 0 . 6 in your formula the resulting area value is precisely the same as mine. You probably deserve credit for your answer, since the discrepancy comes about through no fault of your own.
Please tell me where i am wrong
First of all i have found <HDI and after that i hav simply subtracted area DLM from HDI but my ans is different from your answer my ans which is coming is exactly 580
Log in to reply
After reading your comment, I realized that referring to region H D I as a sector was incorrect, so I've just edited my solution to mention "region H D I " wherever I previously wrote "sector H D I ." A sector by definition is a pie-shaped section of a circle defined by the center of a circle and an arc on that circle's circumference. With region H D I the arc H I does not have vertex D as its center but instead has O (as defined in my solution) as its center, and so region H D I is not technically a sector.
This makes a big difference in how we calculate the area of region H D I , since we can't just use the usual sector area formula, (i.e., the one used for calculating the area of sector D L M .) This is why I took the approach I did in calculating the area of region H D I . Without seeing more details of your solution method, I'm guessing that you may have considered region H D I as a sector, which would have lead to a lesser value for the area of the shaded region.
Let O be the center of the circle, (and hence square as well). Then the area of the "crust" is the area of region D H I minus that of sector D L M .
Now region D H I is composed of quadrant O H I and congruent triangles Δ D H O and Δ D I O . The area of this sector is then
4 π ( O H ) 2 + 2 ∗ 2 1 ( O H ) ( D J ) = 2 5 0 0 ( 1 + 4 π ) .
Next, since ∠ C D I = ∠ A D H = tan − 1 ( 2 1 ) we have that
∠ H D I = 2 π − 2 tan − 1 ( 2 1 ) .
Thus the area of sector D L M is 2 1 ( D C ) 2 ( ∠ H D I ) .
The area of the pizza crust is then
2 5 0 0 ( 1 + 4 π ) − 5 0 0 0 ( 2 π − 2 tan − 1 ( 2 1 ) ) ,
which comes out to 1 2 4 8 . 7 5 when the given values for π and tan − 1 ( 2 1 ) are plugged in, the nearest integer to which is 1 2 4 9 .