Perplexing Rope
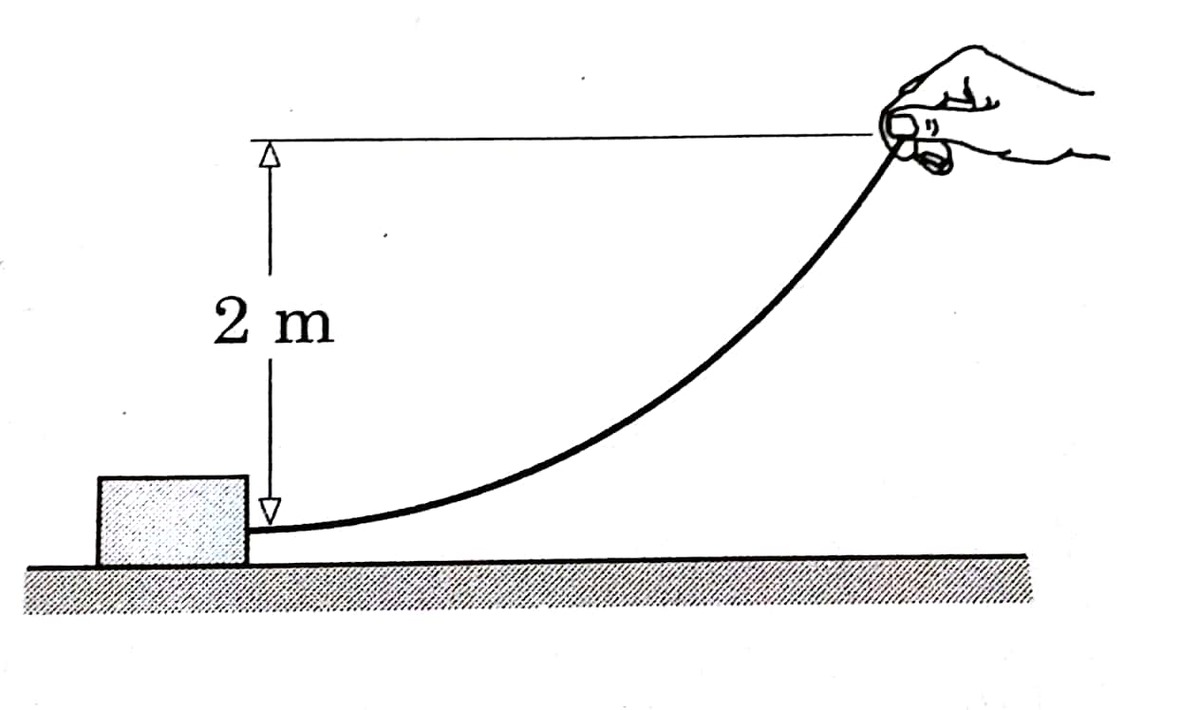
The lower end of a uniform inextensible rope of mass m and length ℓ is attached to a block of mass M placed on a horizontal floor. The coefficient of static friction between the block and floor is μ .
The upper end of the rope is held at height h above the lower end so that the tangent at the lower end remains horizontal as shown. The block is at rest.
(A) Let the angle at which the upper end of rope should be held be α above horizontal. What is cos α ?
(B)What is the magnitude of frictional force between the block and floor in this case? Let it be β N.
(C)Now the upper end of the rope is slowly shifted downward and simultaneously away from the block maintaining the tangent at the lower end horizontal. When it just begins to slide, at what height above the lower end is the upper end? Let it be γ m .
Enter your answer as ⌊ 5 cos α + β + 4 γ ⌋ where ⌊ x ⌋ denotes the last integer not exceeding x .
Details and Assumptions
m = 3 kg
M = 2 0 kg
μ = 0 . 2
h = 2 m
ℓ = 5 m
g = 1 0 m/s 2
This problem is not original.
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry, I'm a bit unclear on the step where you linearize the equations and let δ θ → 0 , how exactly did you arrive at the equations following this statement?
Log in to reply
Expand, and throw away all terms of order δ θ 2 or worse: ( T + δ T ) ( cos θ − sin θ δ θ ) − T cos θ δ T cos θ − T sin θ δ θ δ θ δ T cos θ − T sin θ ≈ 0 ≈ 0 ≈ 0 Now let δ θ → 0 . SImilarly for the second equation...
@Mark Hennings sir please help with this problem discussion on a David Morin Question.
Hint and Answers:-
Tension in the rope varies with height y above lower end as T ( y ) = T ( 0 ) + m g y / ( ℓ ) ⋯ ⋯ ( 1 ) .
Using this with Free body diagram of rope and block, cos α = ℓ 2 + h 2 ℓ 2 − h 2 friction = T ( 0 ) = 2 ℓ h m g ( ℓ 2 − h 2 ) H = γ = m − μ M ℓ + ( μ M ) 2 + m 2 Consider the free body diagram of a small element of the rope.
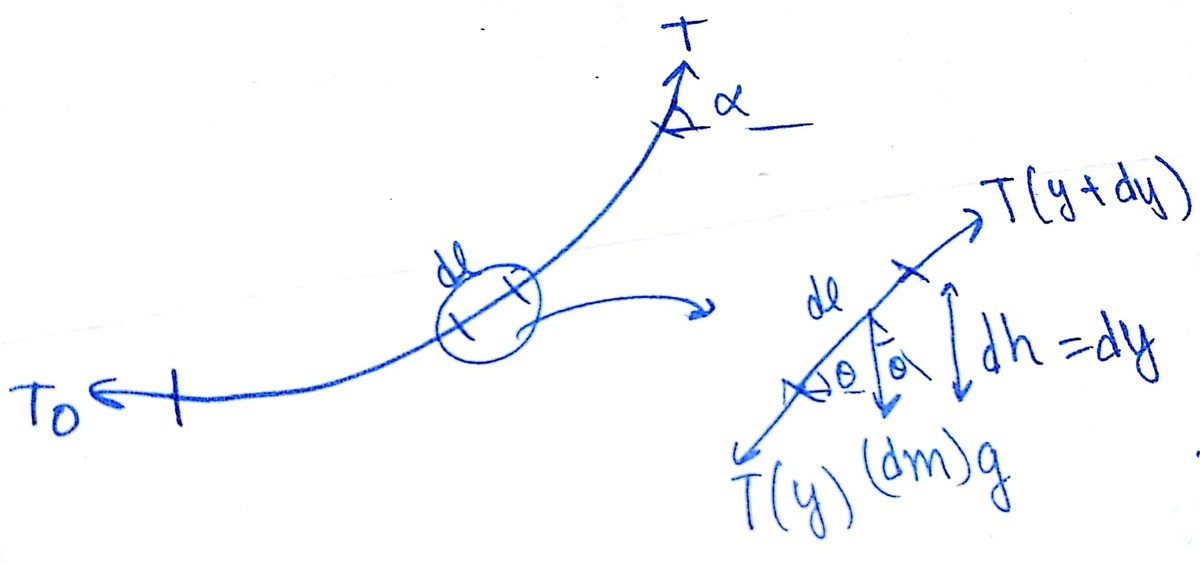 Free Body Diagram
Resolving forces along (parallel to) the element,
T
(
y
+
d
y
)
−
T
(
y
)
=
(
d
m
)
g
sin
θ
=
λ
g
d
y
⟹
d
y
d
T
=
λ
g
∫
T
(
0
)
T
(
y
)
d
T
=
λ
g
∫
0
y
d
y
⟹
(
1
)
.
where
λ
≡
d
ℓ
d
m
is the linear mass density.
Free Body Diagram
Resolving forces along (parallel to) the element,
T
(
y
+
d
y
)
−
T
(
y
)
=
(
d
m
)
g
sin
θ
=
λ
g
d
y
⟹
d
y
d
T
=
λ
g
∫
T
(
0
)
T
(
y
)
d
T
=
λ
g
∫
0
y
d
y
⟹
(
1
)
.
where
λ
≡
d
ℓ
d
m
is the linear mass density.
Now for the whole rope in stasis, T sin α = m g , T cos α = T ( 0 )
This can be used to solve for T ( 0 ) and cos α .
For the third part, set T ( 0 ) = μ M g and express T ( 0 ) as a function of height H of the upper end using equation (1) .
How do you get the value of c o s α ?
Strictly speaking, the angle that T ( y + d y ) makes with the horizontal is θ + d θ , but that yields a negligible error as d θ → 0 .
How do you got the 1st equation
Log in to reply
I have derived it in the text following the picture in the solution.
how did u get the value of cos alpha?
Fix a coordinate system with the origin at the point where the string meets the block. At some point on the string, let θ be the angle that the tangent to the string makes with the horizontal, and let s the arc-length of the string from the origin. In other words, ( s , θ ) are the intrinsic coordinates of the string. Considering the small length of string between θ and θ + δ θ , and resolving forces horizontally and vertically, we have ( T + δ T ) cos ( θ + δ θ ) − T cos θ ≈ 0 ( T + δ T ) sin ( θ + δ θ ) − T sin θ ≈ ℓ m g δ s Linearising, and letting δ θ → 0 , we deduce that d θ d T = T tan θ ℓ m g d θ d s = d θ d T sin θ + T cos θ and hence T = A sec θ s = c tan θ w h e r e c = m g A ℓ But then sec θ = d x d s = c sec 2 θ d x d θ ⇒ d θ d x = c sec θ ⇒ x = c ln ( sec θ + tan θ ) and hence sec θ = cosh ( c x ) and tan θ = sinh ( c x ) , so that s = c sinh ( c x ) . But then c d x d y = c tan θ = s = c sinh ( c x ) , so that y = c ( cosh ( c x ) − 1 ) But this implies that ( y + c ) 2 − s 2 = c 2 , so that s 2 − y 2 = 2 c y and, in addition, T = A cosh ( c x ) = A ( 1 + c y ) , so that T = A + ℓ m g y
We have m = 3 , h = 2 , ℓ = 5 and g = 1 0 . Thus c = 4 1 ( 5 2 − 2 2 ) = 4 2 1 , so that A = ℓ m g c = 2 6 3 . The maximum tension in the string is T = A + ℓ m h g = 2 8 7 , making cos α = T A = 2 9 2 1 . The tension at the bottom of the string must equal the frictional force on the block, and so β = A = 2 6 3 .
In the new configuration we must have A = μ M g = 4 0 , and so c = m g A ℓ = 3 2 0 . Then ( h + c ) 2 = c 2 + ℓ 2 , and hence h = 3 5 , and so γ = 3 5 .
Thus 5 cos α + β + 4 γ = 1 7 4 7 2 7 1 . Taking the integer part of this, we obtain the answer 4 1 .