Perturbation theory
The one-dimensional motion of a particle obeys the dimensionless differential equation x ¨ ( t ) + ε ⋅ ( x ˙ ( t ) ) 2 = 1 where 0 < ε ≪ 1 is an unknown, which describes the strength of the friction force. Initial conditions are x ( 0 ) = x ˙ ( 0 ) = 0 .
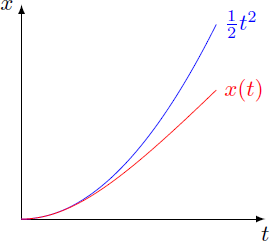
Without friction ( ε = 0 ) there is a movement with constant acceleration, so that the following solution results: x ( t ) = ∫ 0 t ( ∫ 0 t 1 d t ) d t = 2 1 t 2 The general solution can be written in the form x ( t ) = 2 1 t 2 + ε c 1 t 4 + ε 2 c 2 t 6 + … where the c k ∈ R , k ∈ N are unknown parameters .
What is the value of the ratio c 1 c 2 ?
Take care of possible signs!
The answer is -0.266667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We assume, that we can expand the solution as a power series for the parameter ε x ( t ) = x 0 ( t ) + ε ⋅ x 1 ( t ) + ε 2 ⋅ x 2 ( t ) + … = k = 0 ∑ ∞ ε k ⋅ x k ( t ) where the x k ( t ) are functions, which are independant of ε . Since ε is small, we can get a suitable approximations for x ( t ) , if we evaluate a few partial sums.
Inserting the power series into the differential equation results ⇒ ⇒ ⇒ k = 0 ∑ ∞ ε k ⋅ x ¨ k + ε ( k = 0 ∑ ∞ ε k ⋅ x ˙ k ) 2 k = 0 ∑ ∞ ε k ⋅ x ¨ k + k = 1 ∑ ∞ ε k ⋅ i + j = k − 1 ∑ x ˙ i x ˙ j ( x ¨ 0 − 1 ) + k = 1 ∑ ∞ ε k ⋅ ⎝ ⎛ x ¨ k + i + j = k − 1 ∑ x ˙ i x ˙ j ⎠ ⎞ ( x ¨ 0 − 1 ) + ε ⋅ ( x ¨ 1 + x ˙ 0 2 ) + ε 2 ⋅ ( x ¨ 2 + 2 x ˙ 0 x ˙ 1 ) + ⋯ + = 1 = 1 = 0 = 0 Since this must valid for any ε , all expressions inside parentheses must be zero. Therefore, we get a sequence of differential equations x ¨ 0 − 1 x ¨ 1 + x ˙ 0 2 x ¨ 2 + 2 x ˙ 0 x ˙ 1 ⋮ = 0 = 0 = 0 We get the solutions one by one through integration with initial conditions x k ( 0 ) = x ˙ k ( 0 ) = 0 x 0 x 1 x 2 = ∫ ( ∫ 1 d t ) d t = 2 1 t 2 = ∫ ( ∫ ( − x ˙ 0 2 ) d t ) d t = − ∫ ( ∫ t 2 d t ) d t = − 1 2 t 4 = ∫ ( ∫ ( − 2 x ˙ 0 x ˙ 1 ) d t ) d t = ∫ ( ∫ 3 2 t 4 d t ) d t = 4 5 t 6 The final result is of the form x ( t ) = 2 1 t 2 − ε 1 2 t 4 + ε 2 4 5 t 6 + … with the coefficients c 1 = − 1 2 1 and c 2 = 4 5 1 , so that c 1 c 2 = − 4 5 1 2 = − 1 5 4 = − 0 . 2 6 6 6 … .
Disregard my previously posted comment
Take the expansion and calculate the first and second derivatives:
x = 2 1 t 2 + ε c 1 t 4 + ε 2 c 2 t 6 + . . .
x ˙ = t + 4 ε c 1 t 3 + 6 ε 2 c 2 t 5 + . . .
x ¨ = 1 + 1 2 ε c 1 t 2 + 3 0 ε 2 c 2 t 4 + . . .
We will insert this to the original equation of motion x ¨ + ε x ˙ 2 = 1 , and we will compare the coefficients of the t 2 and t 4 terms (as long as we are interested only in c 1 and c 2 , we do not need to go to higher orders). For that we need the t 2 and the t 4 terms in x ˙ 2 ,
x ˙ 2 = ( t + 4 ε c 1 t 3 + 6 ε 2 c 2 t 5 + . . . ) 2 = t 2 + 8 ε c 1 t 4 + . . .
Finally we get
( 1 + 1 2 ε c 1 t 2 + 3 0 ε 2 c 2 t 4 + . . . ) + ( ε t 2 + 8 ε 2 c 1 t 4 + . . . ) = 1
This is satisfied if 1 2 c 1 + 1 = 0 and 3 0 c 2 + 8 c 1 = 0 . The second equation yields c 2 / c 1 = − 4 / 1 5 .