Pete's Probability Procedure 3
Your friend Pete has a stall at the local fete.
As shown below, he has a square board ABCD with a centre O to which a spinner is attached. There are also 6 regions labelled as shown which each make an angle of 6 0 ∘ at the centre (i.e. ∠ EOF = ∠ FOG = . . . = 6 0 ∘ ) and E is the midpoint of AB .
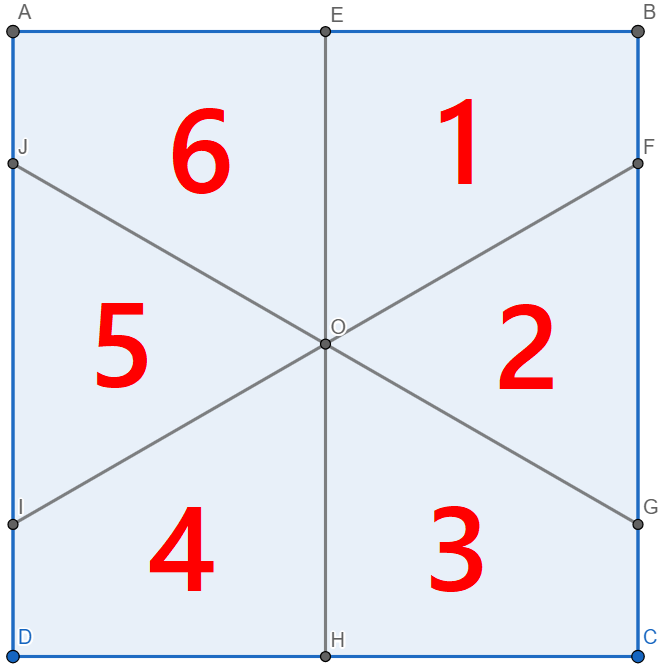
The game is as follows:
The players wear a blindfold. They both spin the spinner and throw a dart at the board. They win if they have obtained both a prime number and a square number (it doesn't matter which out of the spinner or dart got the prime or square, just one of each is needed). What is the probability that a player wins the game?
Details and assumptions:
- The spinner has an equal chance of pointing in any direction
- The location of the dart is uniformly random, and will always hit the board
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Extremely elegant solution! I hadn't thought of doing it this way, but it seems much easier when you look at it like this. You must have wondered why most of the options involved root 3, since your method removed the need for any of that which is simple and elegant
Log in to reply
While this is indeed a very elegant solution as 2 x + 4 y = 1 can be directly substitued, there couldn't have been any way of knowing that 2 x + 4 y would get generated, right?
Log in to reply
I don't think so, without already knowing the answer?? As x and y involve root 3, I think the only cases when this substitution would work is when it is a rational answer? Not sure though
It is interesting to note that the probabilility distribution is different for the numbers in the case of spinner versus the case of the dart.
This can be understood in the following manner:
The spinner rotates about the point and is free to land in any direction, so it can be analysed in terms of the angle spanned by the shape at the vertex. Since all the angles are equal, this gives us: P s ( 1 ) = P s ( 2 ) = P s ( 3 ) = P s ( 4 ) = P s ( 5 ) = P s ( 6 ) = 6 1 where P s ( n ) denotes the probability that the spinner will land on n .
The dart, however has more freedom and this can intuitively understood by oberving that the region of 1 , 3 , 4 , 6 are bigger than the other ones. So, the probability here will be unequal and can be calculated by calculating the relative area of each region. If the side length of the square is 2 , it can be seen that the area of the triangle containing 2 is 3 1 , so the probability of the dart landing in region 2 is 4 3 1 . By symmetry and the fact that total probability is 1, it can be calculated that: P d ( 1 ) = P d ( 3 ) = P d ( 4 ) = P d ( 6 ) = 4 1 − 8 3 1 , P d ( 2 ) = P d ( 5 ) = 4 3 1 where P d ( n ) denotes the probability that the spinner will land on n .
Since the questions states that it doesn't matter which out of the spinner or dart got the prime or square, just one of each is needed, we have two cases:
- Spinner lands on prime, dart lands on square.
- Spinner lands on square, dart lands on prime.
(Since no number is both a square and a prime, we need not worry about any other case.) Primes: 2, 3, 5 Squares: 1, 4
∴ Required probability= ( P s ( 2 ) + P s ( 3 ) + P s ( 5 ) ) ( P d ( 1 ) + P d ( 4 ) ) + ( P d ( 2 ) + P d ( 3 ) + P d ( 5 ) ) ( P s ( 1 ) + P s ( 4 ) )
= ( 2 1 ) ( 2 1 − 4 3 1 ) + ( 3 1 ) ( 4 1 + 8 3 3 )
= 4 1 + 1 2 1
= 3 1
Good solution. I kept getting lots of 3 when I was fiddling around with this problem, but I wanted to make it a rational answer, so the prime and square part seemed to fit miraculously, so that's only when I decided what to make the actual question of the problem!
Log in to reply
I too was quite surprised to see the 3 terms cancelling out!
Let x be the probability of getting a 2 or 5 with the dart, and let y be the probability of getting a 1, 3, 4, or 6 with the dart. Then 2 x + 4 y = 1 .
A player wins in the following cases: dart 2 2 3 3 5 5 1 1 1 4 4 4 spinner 1 4 1 4 1 4 2 3 5 2 3 5 probability 6 x 6 x 6 y 6 y 6 x 6 x 6 y 6 y 6 y 6 y 6 y 6 y
Adding up the probabilities, we get that the overall probability of winning is 4 ⋅ 6 x + 8 ⋅ 6 y = 6 4 x + 8 y = 6 2 ( 2 x + 4 y ) = 3 1 .