Petroleum permittivity

Since the angle is the same, the ratio of the electric force to the net vertical force must be the same. Since the permittivity increases by a factor of 2, the electric force decreases by a factor of two. Therefore, the buoyant force from the liquid must effectively nullify half of the gravitational force on each ball. This means that the fluid must be half as dense as the ball. The answer is therefore $2 \times 800 = 1600$

Let’s look at the force diagrams. The ball on the left has a full tension vector while the left one has the same tension in x and y components. Since both balls are stationary in this position the net force must equal 0. The same works for the case in the fluid - but we must include the buoyant force, new weight: $G’ = mg - \rho gV$

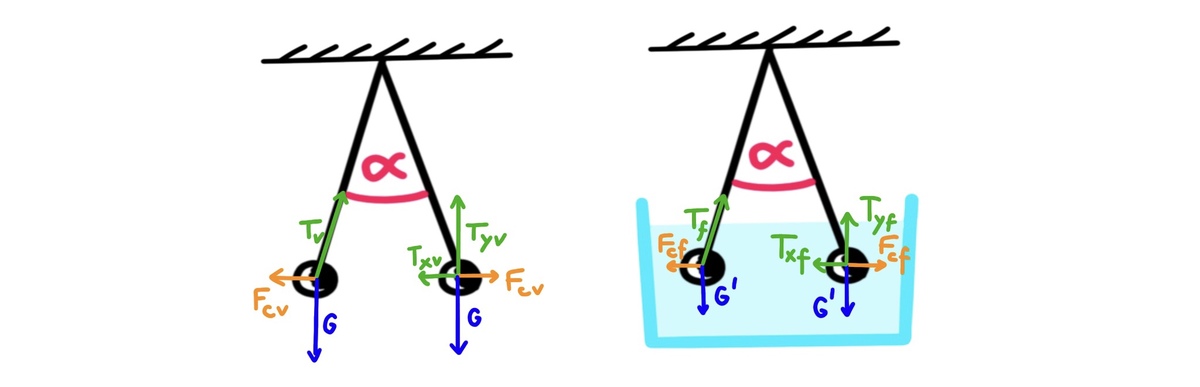
The angles between forces and strings remain the same so we have two similar triangles, one from the left force diagram and the other from the right one. The ratio of forces $T_{xv}$ and $T_{yv}$ is equal to the ratio of forces $T_{xf}$ and $T_{yf}$ :

$\frac{T_{xv}}{T_{yv}} = \frac{T_{xf}}{T_{yf}}$

We know that $T_{xv} = F_{cv} = k\frac{Q^2}{r^2}$ and $T_{yv} = G = mg$

Also, we know $T_{xf} = F_{cf} = \frac{k}{\varepsilon_r}\frac{Q^2}{r^2}$ and $T_{yf} = G’ = mg - \rho gV$

Now we can just substitute:

$\frac{k\frac{Q^2}{r^2}}{mg} = \frac{\frac{k}{\varepsilon_r}\frac{Q^2}{r^2}}{mg - \rho gV}$ $\to$ $\frac{1}{m} = \frac{\frac{1}{\varepsilon_r}}{m - \rho V}$ $\to$ $\frac{1}{m} = \frac{1}{\varepsilon_r(m - \rho V)}$ $\to$ $m = \varepsilon_r(m - \rho V)$ $\to$ $m = 2m - 2\cdot800V$ $\to$ $m = 1600V$

We know that $\rho_B = \frac{m}{V}$ , so $V=\frac{m}{\rho_B}$ therefore $m = 1600\cdot \frac{m}{\rho_B}$ or $1 = \frac{1600}{\rho_B}$

$\rho_B = 1600\text{ kg/m}^3$