Phase Angle for Max Power
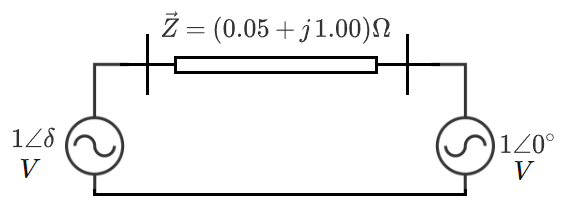
Two ideal AC voltage sources are connected to each other through a complex impedance, as shown in the diagram. What value of the left source phase angle ( δ ) maximizes the active power consumed by the source on the right?
Give your answer in degrees, to 2 decimal places.
The answer is 87.14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for the solution. The result ends up being the same as the impedance angle. I thought that was interesting.
Voltage on the impedance is the difference between them:
V = 1 ∠ δ − 1 ∠ 0
V = [ cos ( δ ) − 1 ] + j sin ( δ )
Current on the impedance is the same current of the whole cicruit:
I = 0 . 0 5 + j V
I = 1 . 0 0 2 5 [ 0 . 0 5 ( cos ( δ ) − 1 ) + sin ( δ ) ] + j [ ( cos ( δ ) − 1 ) − sin ( δ ) ]
Power on the right source is:
S = 1 ∠ 0 ⋅ I ∗
S = 1 . 0 0 2 5 [ 0 . 0 5 ( cos ( δ ) − 1 ) + sin ( δ ) ] + j [ ( cos ( δ ) − 1 ) − sin ( δ ) ]
Active power is:
P = ℜ ( S )
P = 1 . 0 0 2 5 0 . 0 5 ( cos ( δ ) − 1 ) + sin ( δ )
Differentiating P with respect to δ and making it equal to 0 :
d δ d P = 1 . 0 0 2 5 − 0 . 0 5 sin ( δ ) + cos ( δ ) = 0
tan ( δ ) = 2 0
δ = tan − 1 ( 2 0 ) or δ = tan − 1 ( 2 0 ) + 1 8 0 o
However, the second derivative of P with respect to δ :
d δ 2 d 2 P = 1 . 0 0 2 5 − 0 . 0 5 cos ( δ ) − sin ( δ )
Is negative on tan − 1 ( 2 0 ) (maximum) and positive on tan − 1 ( 2 0 ) + 1 8 0 o (minimum)
Hence the solution is:
δ = tan − 1 ( 2 0 ) ≈ 8 7 . 1 4 o
Nice solution. It's the same as the impedance angle.
The current I through the circuit is given by:
I = Z 1 ∠ δ − 1 ∠ 0 ∘ = 0 . 0 5 + j 1 . 0 0 cos δ + j sin δ − 1 = ( 0 . 0 5 + j 1 . 0 0 ) ( 0 . 0 5 − j 1 . 0 0 ) ( cos δ − 1 + j sin δ ) ( 0 . 0 5 − j 1 . 0 0 ) = 1 . 0 0 2 5 0 . 0 5 ( cos δ − 1 ) + sin δ + j ( 0 . 0 5 sin δ − cos δ + 1 )
The active power consumed by the source on the right is maximum when ℜ ( I ) is maximum. That is when 0 . 0 5 cos δ + sin δ is maximum.
f ( δ ) f ′ ( δ ) ⟹ tan δ ⟹ δ = 0 . 0 5 cos δ + sin δ ) = − 0 , 0 5 sin δ + cos δ = 0 . 0 5 1 = 2 0 ≈ 8 7 . 1 4 ∘ Equating f ′ ( δ ) = 0
Note that f ′ ′ ( 8 7 . 1 4 ∘ ) < 0 . Therefore the active power consumed by the source on the right is maximum when δ ≈ 8 7 . 1 4 ∘ .