Physics in throwing a ball
Have you ever thrown a ball a ball? Your answer would be most probably yes. But have you ever wondered what shape does the flight of ball has? You may say that the ball travels on a arc type path of a circle or ellipse when thrown. But do you know what this shape is called? It is called a "parabola".
This shape in which ball is thrown has a unique mathematics and science hidden in it. Let's look at them.
1. The downfall of ball:
The ball when reaches it's peak then start's fall down and the rate at which it falls down is very interesting.

Firstly, after one second its falls down at the speed of 5 m/s and after another one second at the speed of 15 m/s and so on. Thus, the ball accelerates at the speed of 10 m/s. And another fact that the ball only goes in this order and this happens due to the Earth's gravitational pull. So, the ball will travel 1/6 times less on Moon and also will also accelerates 1/6 times slower (as the gravity of moon is 1/6 times weaker than that of Earth). This rate on other planets and celestial bodies can also be shown in a table just like the table given below.
| Mercury | Venus | Earth | Moon | Mars | Jupiter | Saturn | Uranus | Neptune |
| ~3 m/s velocity | >4 m/s velocity | 5 m/s velocity | <1 m/s velocity | ~3 m/s velocity | ~12.5 m/s velocity | >5 m/s velocity | <5 m/s velocity | >5 m/s velocity |
| ~6 m/s acceleration | >8 m/s acceleration | 10 m/s acceleration | <2 m/s acceleration | ~6 m/s acceleration | ~25 m/s acceleration | >10 m/s acceleration | <10 m/s acceleration | >10 m/s acceleration |
Thus, we can conclude that the length of the parabola can be counted by counting the seconds of the ball in fight and then dividing it by 2 and then counting the velocity in each second by knowing the acceleration rate of 10 m/s and adding it and then multiplying it by two (as the downfall of ball is it's half length of distance) and now we get the answer. But this might confuse you so let's make it easy by making a formula like this:
Parabola's length = and then 1st s + 2nd s + 3rd s +..... = )
Note: In this equation the letter s refers to second.
2. Parabola's peak height is equivalent to parabola's downfall length
There is an interesting thing in parabola that it's peak height is equivalent to it its half length. This means that we can find the height of a parabola's peak by just knowing the downfall length of parabola or what about only knowing the downfall's time. This can be done by the following equation.
Parabola's peak height =
As the shape of thrown ball's path is also parabola, this rule can be applied to find the height of the ball by counting the seconds of downfall.
3. Atmospheric pressure and it's effect to the ball
Now let's see how much the angle should be to throw a ball to the maximum distance. And the answer is that the angle should less than 45 degrees angle or may be even less. So that's clear but atmospheric pressure joins the show ruins everything. If you can throw a ball that goes about 40 m then it could go about 300 m without atmospheric pressure or with a light atmospheric pressure.
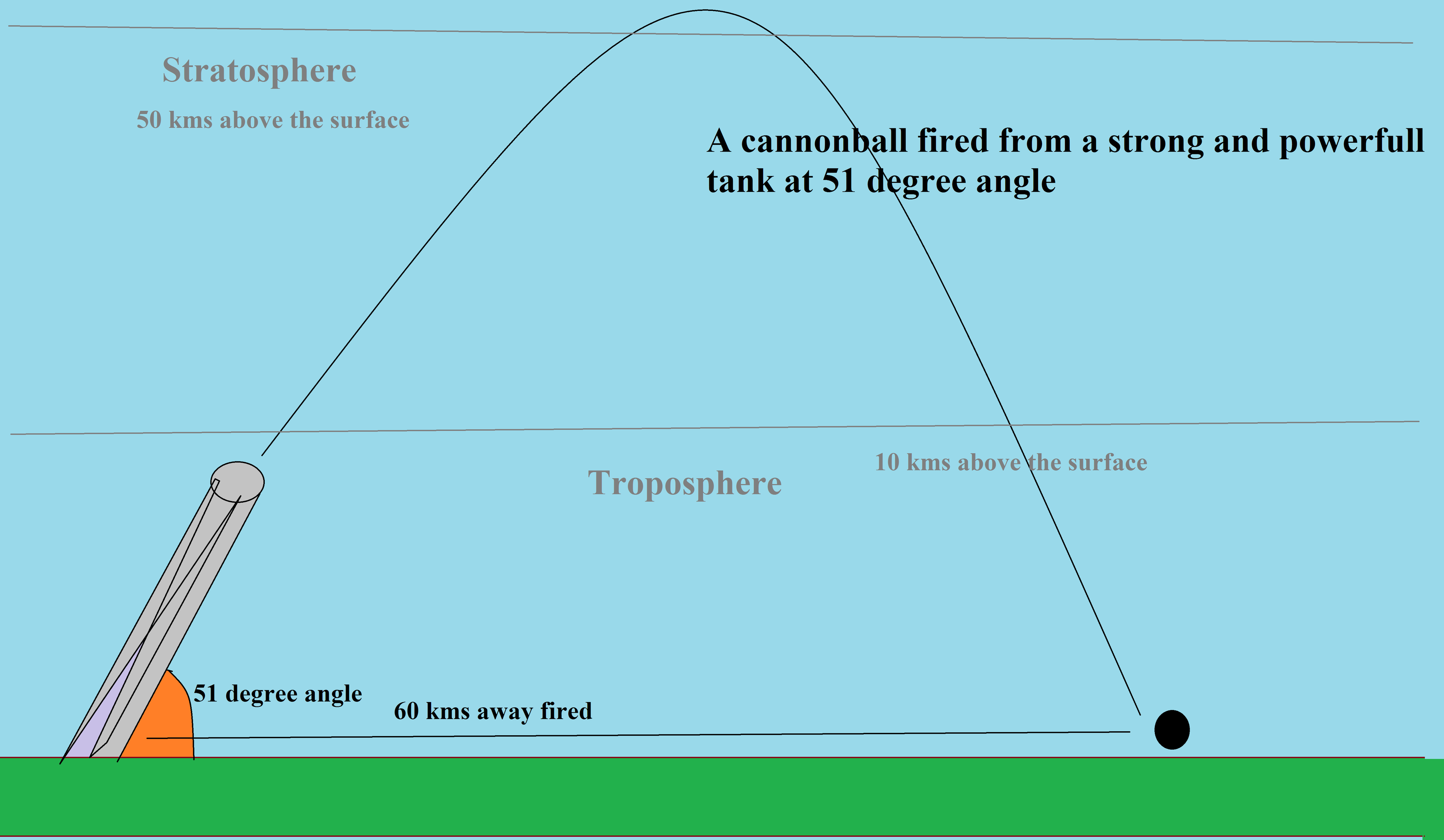
So, what's the solution? You might be thinking. So, there is a solution but it works for extra large and great army cannons only and not with your hand or something like that. It is that throw the cannonball at 51 degrees so that it reaches stratosphere which has a very low atmospheric pressure and reaches at maximum distance.
This idea was also been done by Germany during World War I or may be II. Germany had a very big tank for the battle but it couldn't fire cannonballs to huge distances so after some suggestions the cannon wold fire cannon balls at 51 degrees and would throw the ball to up to 60 km. By knowing all this let's look at the today's problem.
Today's problem:
If you are on moon (obviously not in reality just imagine it) and if you throw a ball that goes at a distance of 2 km with peak height of 501 m then find the time taken for the downfall. And keep this things in note:
- The Moon's gravity is 1/6th so let's consider the velocity of first second to be 1 and acceleration 2 .
- There is no atmospheric pressure on moon.
Hint: You can reverse a formula to find the answer
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
ERROR