Physics isn't fun without calculus!

Classical Mechanics Level 3

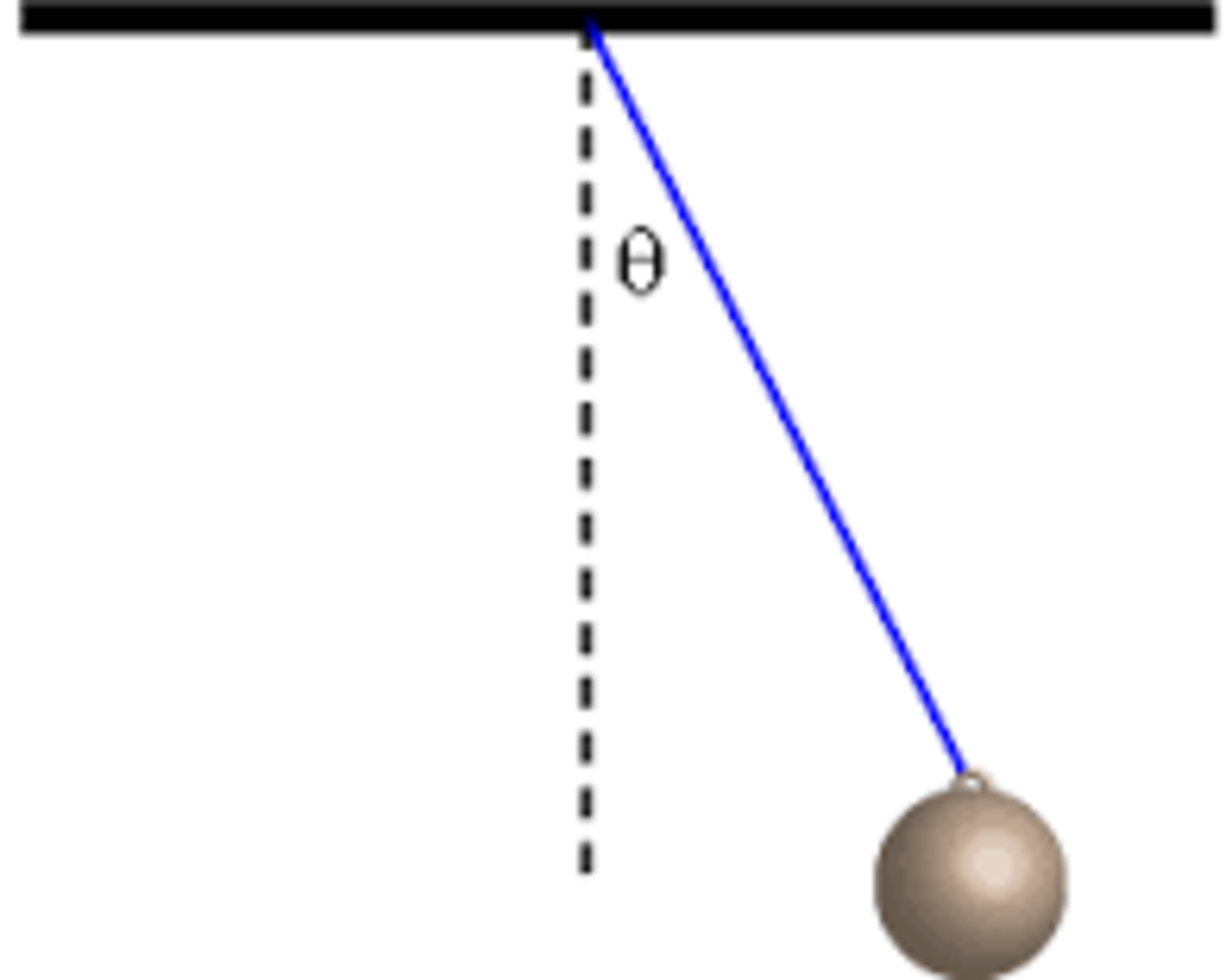
The figure below shows a simple pendulum formed of a rod of negligible mass suspending at its lower end a particle (P).The pendulum is shifted by an angle $\theta$ from its stable equilibrium position in the vertical plane. Friction is not neglected.Assume that at the end of each oscillation of the system, the amplitude ( $\theta$ ) is divided by the same factor $b=1.025$ . Determine the number of the oscillations described by the oscillator during the time needed by the amplitude to drop from ${ 10 }^{ \circ }$ to ${ 6.9 }^{ \circ }$ .

10 5.8 7.5 15

1 solution

Mohammad Hamdar
Jan 8, 2016

$\\ \\ \\ { t }_{ 0 }\quad :\quad amplitude\quad { \theta }_{ 0 }={ 10 }^{ \circ }\\ t=T\quad :\quad amplitude\quad { \theta }_{ 1 }=\frac { { \theta }_{ 0 } }{ b } \\ t=2T\quad :\quad amplitude\quad { \theta }_{ 2 }=\frac { { \theta }_{ 0 } }{ { b }^{ 2 } } \\ t=nT\quad :\quad amplitude\quad { \theta }_{ n }=\frac { { \theta }_{ 0 } }{ { b }^{ n } } \\ { \theta }_{ n }={ 6.9 }^{ \circ }\quad ,\quad { \theta }_{ 0 }={ 10 }^{ \circ }\\ 6.9=\frac { 10 }{ { (1.025) }^{ n } } \quad ,\quad \ln { { (1.025) }^{ n } } =ln(\frac { 10 }{ 6.9 } )\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad n=\frac { \ln { (1.449) } }{ \ln { (1.025) } } =15\quad oscillations.$

Physics isn't fun without calculus!

1 solution

0 pending reports