Physics through Omega.
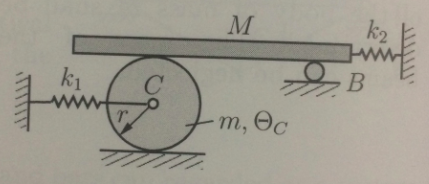
A wheel ( mass , moment of inertia , radius ) rolls without slipping on a flat surface. On its top, the wheel carries a horizontally guided beam ( mass ) and moves it without slipping.
Determine the angular frequency of the system in S.I. units . Neglect the mass of guiding roll .
Given : , , , , , .
The answer is 1.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Several key points to note about this problem:
1) The wheel has both rotational and translational kinetic energy
2) The beam has twice the translational speed as the wheel's center of mass. This is because the speed (from CM translation + rotation) at the top of the wheel is twice the translational speed of the wheel's center of mass.
3) The left spring is stretched (if the wheel moves rightward), and the right spring is compressed by twice the distance by which the left spring is stretched. Despite the fact that one is stretched and the other is compressed, the potential energies associated with both are positive.
Note: I will use θ as the rotation angle and I as the wheel moment of inertia.
Kinetic Energy:
E = 2 1 m r 2 θ ˙ 2 + 2 1 I θ ˙ 2 + 2 M r 2 θ ˙ 2
Potential Energy:
U = 2 1 k 1 r 2 θ 2 + 2 k 2 r 2 θ 2
Lagrangian:
L = E − U = 2 1 m r 2 θ ˙ 2 + 2 1 I θ ˙ 2 + 2 M r 2 θ ˙ 2 − 2 1 k 1 r 2 θ 2 − 2 k 2 r 2 θ 2
Equation of Motion:
d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L
Evaluation: [ m r 2 + I + 4 M r 2 ] θ ¨ = − [ k 1 r 2 + 4 k 2 r 2 ] θ
This corresponds to simple harmonic motion with the following angular frequency:
ω = m r 2 + I + 4 M r 2 k 1 r 2 + 4 k 2 r 2 = I + ( m + 4 M ) r 2 ( k 1 + 4 k 2 ) r 2
Plugging in numbers gives ω = 1 . 2 5 rad/s