Pi and Pythagorean triples

Geometry Level 4

1 8 π ( sin ⁡ − 1 ( 3 5 ) + sin ⁡ − 1 ( 12 13 ) + sin ⁡ − 1 ( 63 65 ) ) = ? \large \frac1{8\pi} \left( \sin^{-1} \left(\frac35\right) + \sin^{-1} \left(\frac{12}{13}\right) + \sin^{-1} \left(\frac{63}{65} \right) \right) = \ ?


The answer is 0.125.

View wiki
Alisa Meier by Alisa Meier , 24, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Let α = sin ⁡ − 1 3 5 \alpha = \sin^{-1} \dfrac{3}{5} , β = sin ⁡ − 1 12 13 \beta = \sin^{-1} \dfrac{12}{13} and γ = sin ⁡ − 1 63 65 \gamma = \sin^{-1} \dfrac{63}{65} .

⇒ { sin ⁡ α = 3 5 cos ⁡ α = 4 5 sin ⁡ β = 12 13 cos ⁡ β = 5 13 sin ⁡ γ = 63 65 cos ⁡ γ = 16 65 \Rightarrow \begin{cases} \sin{\alpha} = \dfrac{3}{5} & \cos{\alpha} = \dfrac{4}{5} \\ \sin{\beta} = \dfrac{12}{13} & \cos{\beta} = \dfrac{5}{13} \\ \sin{\gamma} = \dfrac{63}{65} & \cos{\gamma} = \dfrac{16}{65} \end{cases}

Now we have:

sin ⁡ ( α + β + γ ) = sin ⁡ ( α + β ) cos ⁡ γ + cos ⁡ ( α + β ) sin ⁡ γ = 16 65 ( sin ⁡ α cos ⁡ β + cos ⁡ α sin ⁡ β ) + 63 65 ( cos ⁡ α cos ⁡ β − sin ⁡ α sin ⁡ β ) = 16 65 ( 3 5 × 5 13 + 4 5 × 12 13 ) + 63 65 ( 4 5 × 5 13 − 3 5 × 12 13 ) = 16 65 ( 63 65 ) − 63 65 ( 16 65 ) = 0 \begin{aligned} \sin (\alpha + \beta + \gamma) & = \sin (\alpha + \beta) \cos \gamma + \cos (\alpha + \beta) \sin \gamma \\ & = \frac{16}{65} (\sin \alpha \cos \beta + \cos \alpha \sin \beta) + \frac{63}{65} (\cos \alpha \cos \beta - \sin \alpha \sin \beta) \\ & = \frac{16}{65} \left(\frac{3}{5} \times \frac{5}{13} + \frac{4}{5} \times \frac{12}{13} \right) + \frac{63}{65} \left( \frac{4}{5} \times \frac{5}{13} - \frac{3}{5} \times \frac{12}{13} \right) \\ & = \frac{16}{65} \left(\frac{63}{65} \right) - \frac{63}{65} \left( \frac{16}{65} \right) \\ & = 0 \end{aligned}

⇒ α + β + γ = π ⇒ sin ⁡ − 1 3 5 + sin ⁡ − 1 12 13 + sin ⁡ − 1 63 65 = π ⇒ 1 8 π ( sin ⁡ − 1 3 5 + sin ⁡ − 1 12 13 + sin ⁡ − 1 63 65 ) = 1 8 π × π = 1 8 = 0.125 \Rightarrow \alpha + \beta + \gamma = \pi \\ \Rightarrow \sin^{-1} \dfrac{3}{5} + \sin^{-1} \dfrac{12}{13} + \sin^{-1} \dfrac{63}{65} = \pi \\ \Rightarrow \dfrac{1}{8 \pi} \left( \sin^{-1} \dfrac{3}{5} + \sin^{-1} \dfrac{12}{13} + \sin^{-1} \dfrac{63}{65} \right) = \dfrac{1}{8 \pi} \times \pi = \dfrac{1}{8} = \boxed{0.125}

14 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

You have shown that sin ⁡ ( α + β + γ ) = 0 \sin(\alpha+\beta+\gamma) = 0 , but does that mean that α + β + γ = π \alpha+\beta+\gamma = \pi only? Why can't it equals to 0 , 2 π , 3 π , 4 π , 5 π , … 0,2\pi, 3\pi, 4\pi, 5\pi,\ldots ?

There's a much simpler approach.

Hint : Construct 3 right triangles side by side.

@Calvin Lin , well, he can bound the sum. Since the range of arcsin ⁡ ( x ) \arcsin(x) for positive x x is ( 0 , π 2 ] \left(0,\frac{\pi}2\right] , we have,

α + β + γ ∈ ( 0 , 3 π 2 ] \alpha+\beta+\gamma\in \left(0,\frac{3\pi}2\right]

which ensures that α + β + γ = π \alpha+\beta+\gamma=\pi and not any other integer multiple of π \pi .

Prasun Biswas - 5 years, 10 months ago
Richard Levine
Aug 13, 2015

Note the inserted image.

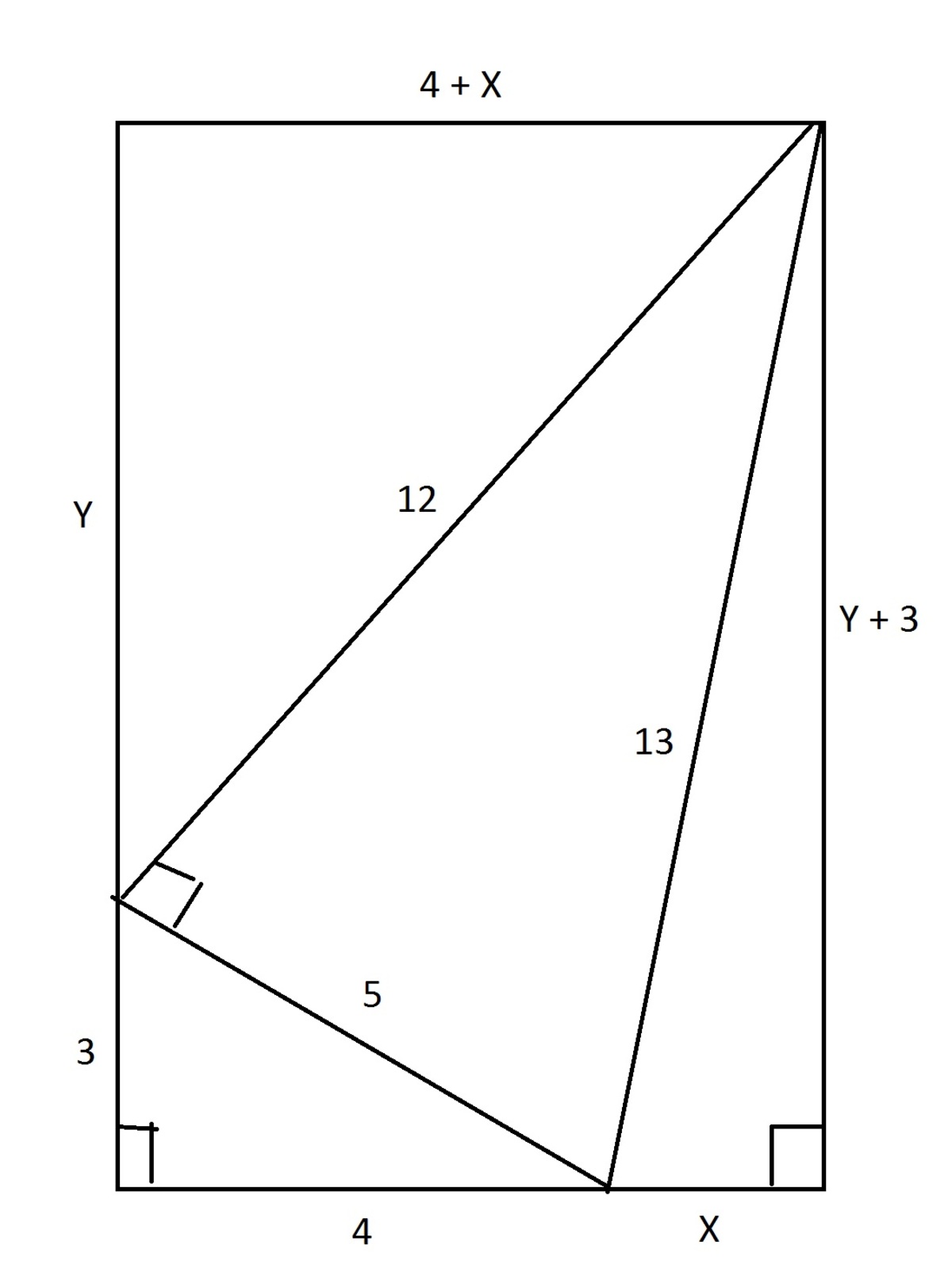
From that rectangle, we can derive the following 2 equations: 1) 12^2 - (4+X)^2 = y^2; 2) 13^2 - (Y+3)^2 = X^2. Subtract one from the other to get x = (3Y-16)/4, then sub back into the second equation to get Y = 9.6. So, Y+3 = 12.6 and X=3.2. That means triangle with sides X, Y+3, 13 is similar to triangle with sides 16, 63, 65, since you can just multiply all sides by 5. This shows that the arcsin sum in this problem is a straight line (the bottom of the rectangle), which is 180 degrees, which is pi. So (1/(8 pi)) pi = 1/8 = .125.

Also, arcsin sum approximation of pi on Wikipedia shows that this arcsin sum in this problem has been used to determine the value of pi. So (1/(8 pi)) pi = 1/8 = .125.

13 Helpful 0 Interesting 0 Brilliant 0 Confused

That's great and all, but you can't really come up with it without already knowing the answer. In reality this is just lucky guess and check. That said, it's still a very nice looking solution.

Alex Li - 5 years, 4 months ago
Andriane Casuga
Aug 13, 2015

The numbers are interesting because they are all parts of triangles made up of Pythagorean triples, which makes the math very easy if you use three acute triangles. The correct answer is 1/8 = 0.125.

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Gregory Lewis
Jul 16, 2016

a = sin' (3/5) => tan (a) = 3/4

b = sin' (12/13) => tan (b) = 12/5

c = sin' (63/65) => tan (c) = 63/16

Using tan (x+y) = (tan (x) + tan (y)) / (1 - tan (x) * tan (y)) twice...

tan (a+b) = (3/4 + 12/5) / (1 - 3/4 * 12/5) = -63/16

tan ((a+b)+c) = (-63/16 + 63/16) / (1 + 63/16 * 63/16) = 0

a+b+c = tan' (0)

Since all three angles are acute, a+b+c = pi.

So (1 / (8 * pi)) * (a+b+c) = 0.125

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...