Pi and triangles? No!

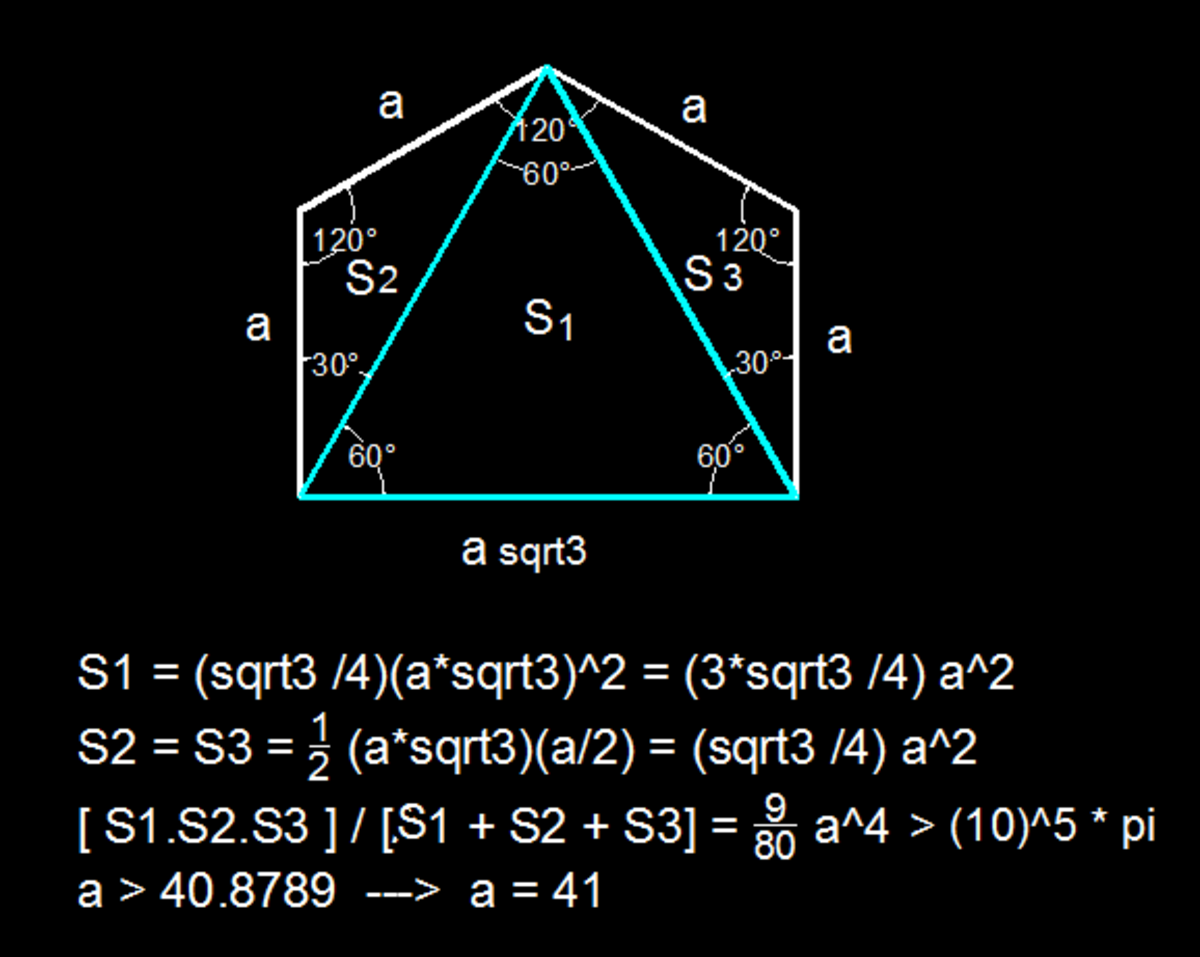
A pentagon has respective side lengths $a$ , $a \sqrt 3$ , $a$ , $a$ , and $a$ , and angles $90^\circ$ , $90^\circ$ , $120^\circ$ , $120^\circ$ , and $120^\circ$ , both corresponding. This pentagon can be split into an equilateral triangle and two other triangles.

Find the smallest positive integer of $a$ which satisfies the condition the product of the areas of the three triangles divided by their sum is greater than $100000 \pi$ .