Pi Day Square and Rectangle

A square with an area of π and a rectangle also with an area of π share the same center and intersect at right angles. The overlapping parts are colored red and the non-overlapping parts are colored blue.
If the combined area of the blue sections is 6 times the area of the red section, then the longest side of the rectangle is n π , where n is an integer.
Find n .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
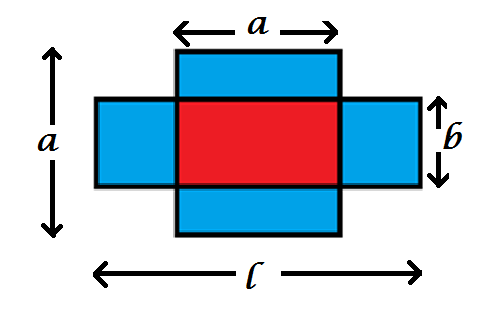
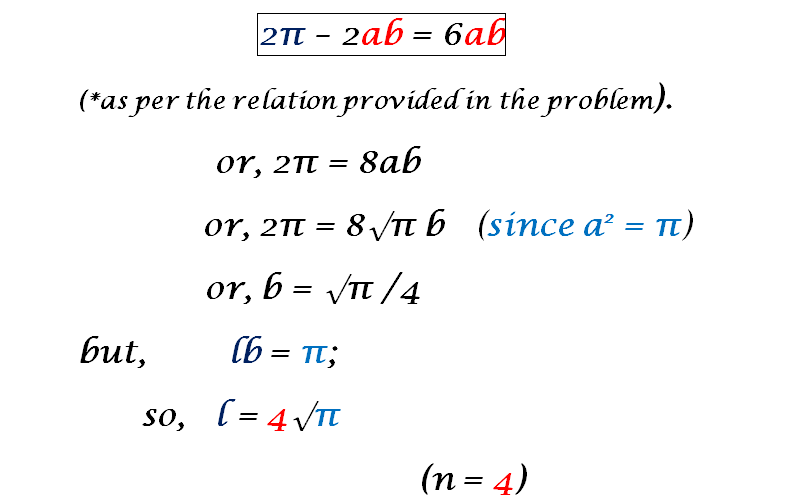
@David Vreken .. pardon me! for the copyright issues :P (*diagram)
Let the red area be A red . Then the blue area A blue = 2 ( π − A red ) and
2 ( π − A red ) π − A red ⟹ A red = 6 A red = 3 A red = 4 π
Since the area of the square A □ = π , the side length of the square is π , which is also the long side length of the red rectangle. Therefore, the short side length of the red rectangle is π 4 π = 4 π , which is also the short side length of the larger rectangle. And the long side length of the rectangle is 4 π π = 4 π ⟹ n = 4 .
Let B be the combined area of the blue sections and R be the area of the red section. Since both rectangle and square have an area of π , B + 2 R = 2 π , and since the area of the blue sections are 6 times the area of the red sections, B = 6 R . These two equations solve to R = 4 1 π .
Since the square has an area of π , its sides are π , so the red section has this side and a side equal to π R = π 4 1 π = 4 1 π , and the rectangle with an area of π has this side and a side equal to 4 1 π π = 4 π . Therefore, n = 4 .
Let
a
,
b
be the longer and shorter lengths of the rectangle,
c
be the side length of the square, and
B
and
R
be the total area of the blue and red rectangles, respectively.
Let
n
be such that
a
=
n
π
. Then since
a
∗
b
=
π
,
b
=
n
π
. Since the square has area
π
,
c
=
π
.
Notice that R = b ∗ c , i.e., R = n π × π = n π .
We can use inclusion-exclusion to get the sum of the areas of the blue rectangles: it is equal to the original rectangle plus the area of the square (each of which is π ) minus twice the area of the red rectangle, i.e.
B = 2 ∗ π − 2 ∗ n π = n 2 ( n − 1 ) π
Since B = 6 R , we have n 2 ( n − 1 ) π = n 6 π , which simplifies to 2 ∗ ( n − 1 ) = 6 , i.e. n = 4 .
Nice solution!
Let the side of the square is c, and the rectangle are a, and b (the longer side). ab=c^2= π Then a(b – c) + c(c – a) = 6 ac. or ab + c^2 – 8 ac = 0, a=(1/4) √π. b = 4√π
Great solution! Thanks for posting!