Doodle Probability
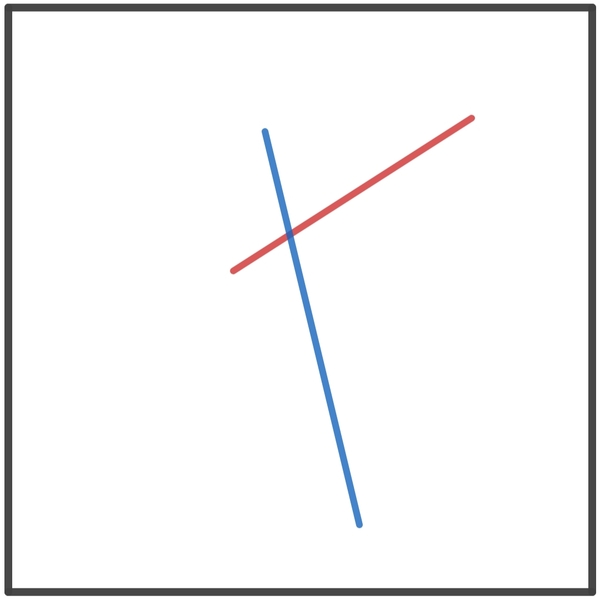
Two points are randomly selected on a square sheet of paper and are joined to form a line segment.
This process is repeated to obtain another line segment.
What is the probability that the two lines intersect?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We start by selecting four points inside the square.
The figure on left shows the cases where the four points have a concave hull (It can be seen that none of the colored configurations intersect).
The figure on right shows the cases where the four points have a convex hull (It can be seen that one out of the three colored configurations intersect).
Hence, the lines segments will intersect if and only if the four points form a convex figure (i.e none of the selected points is inside the triangle formed by the other three)
Let P convex be the probability that the four points form a convex figure.
If a convex figure is obtained, then the probability that the line segments intersect is 3 1 .
If a concave figure is obtained, then the probability that the line segments intersect is 0 .
Hence the probability we are looking for is P = 3 1 × P convex .
Now we need to find P convex .
First, Let's calculate the probability P α that the first point is inside the triangle formed by the other three.
P α = Δ Square E ( Δ Triangle )
where E ( Δ Triangle ) is the expected value of the area of the triangle formed by the three points, and Δ Square is the area of the square.
Same goes for P β , P γ and P δ . Obviously P α = P β = P γ = P δ .
Probability that any point is inside of triangle formed by other three is P α + P β + P γ + P δ = 4 P α because no more than one of these outcomes can happen simultaneously.
P convex = 1 − 4 P α = 1 − 4 E ( Δ Triangle )
Now, we only need to find E ( Δ Triangle ) , which is given by
E ( Δ Triangle ) = ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 d x 1 d x 2 d x 3 d y 1 d y 2 d y 3 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∣ Δ ∣ d x 1 d x 2 d x 3 d y 1 d y 2 d y 3
= ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 2 ∣ − x 2 y 1 + x 3 y 1 + x 1 y 2 − x 3 y 2 − x 1 y 3 + x 2 y 3 ∣ d x 1 d x 2 d x 3 d y 1 d y 2 d y 3 = 1 4 4 1 1
Here, ( x i , y i ) represent the polygon vertices of the triangle for i = 1 , 2 , 3 , and the (signed) area of these triangles is given by the determinant
Δ = 2 ! 1 ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ = 2 1 ( − x 2 y 1 + x 3 y 1 + x 1 y 2 − x 3 y 2 − x 1 y 3 + x 2 y 3 )
⟹ E ( Δ Triangle ) = 1 4 4 1 1
⟹ P convex = 1 − 4 E ( Δ Triangle ) = 3 6 2 5
⟹ P = 3 1 × P convex = 1 0 8 2 5
A better approach on finding E ( Δ Triangle ) can be found here and here
Click here for more information.