Picture this ....
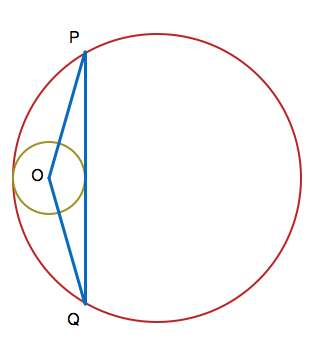 A circle of radius
is internally tangent to a unit circle. A chord is drawn inside the unit circle that is tangent to the radius
circle and perpendicular to the line joining the centers of the two circles.
A circle of radius
is internally tangent to a unit circle. A chord is drawn inside the unit circle that is tangent to the radius
circle and perpendicular to the line joining the centers of the two circles.
Let be the center of the smaller circle, and let be the endpoints of the chord as described above. The value of that maximizes the perimeter of triangle can be written as , where are positive coprime integers and is square-free. Find .
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Just a quick outline of one solution method....
The distance between the center C of the unit circle and the point T of tangency of the chord and the smaller circle is 1 − 2 r . By symmetry, T is the midpoint of the chord, so triangle C T P is a right-angled triangle. By Pythagoras, we have that
T P = 1 − ( 1 − 2 r ) 2 = 2 r − r 2 ,
and so the length of the chord is 4 r − r 2 .
Again using Pythagoras, the lengths of sides O P and O Q are each
r 2 + ( T P ) 2 = r 2 + 4 ( r − r 2 ) = 4 r − 3 r 2 .
The perimeter of triangle O T P is then L = 4 r − r 2 + 2 4 r − 3 r 2 .
Setting the derivative d r d L equal to 0 and then simplifying yields the equation
( 2 r − 1 ) 4 r − 3 r 2 = ( 2 − 3 r ) r − r 2 ,
which, after squaring both sides and further simplifying, yields the equation
3 r 2 − 7 r + 3 = 0 ⟹ r = 6 7 ± 1 3 .
Now since r < 1 we have r = 6 7 − 1 3 . Thus a = 7 , b = 1 3 , c = 6 and a + b + c = 2 6 .
Comment: Since the perimeter would go to 0 as r → 0 it should be clear that any critical point found using the above method will yield a maximum perimeter. An application of the second derivative test would be definitive, but not practically necessary.