Piece of Cake Level Algebra Question

$\begin{aligned} (x-2)^2 + y^2 & = 3 \\ \implies y^2 & = 3 - (x-2)^2 \\ \left(\frac yx\right)^2 & = \frac 3{x^2} - \left(\frac {x-2}x \right)^2 \\ & = \frac 3{x^2} - \left(1-\frac 2x \right)^2 \\ & = \frac 3{x^2} - \left(\frac 4{x^2} -\frac 4x + 1\right) \\ & = - \left(\frac 1{x^2} -\frac 4x + 1\right) \\ & = 3 - \left(\frac 1{x^2} -\frac 4x + 4\right) \\ & = 3 - \left(\frac 1x - 2\right)^2 & \small \color{#3D99F6} \text{Since }\left(\frac 1x - 2\right)^2 \ge 0 \\ \implies \left(\frac yx\right)^2 & \le \boxed 3 & \small \color{#3D99F6} \text{Equality occurs when }x = \frac 12 \end{aligned}$

Let $\frac{y}{x} = k$ , then $y = kx$ $\\$ $(x-2)^2+k^2 x^2 = 3$ $\\$ Rearrange the equation and get $(1 + k^2)x^2 - 4x + 1 = 0$ $\\$ Discriminant $\delta = b^2 - 4ac = 16 - 4(1 + k^2) \geq 0$ $\\$ $\therefore -\sqrt 3 \leq k \leq \sqrt 3$ $\\$ $k_{max} = 3$

We could interpret this geometrically, as maximizing the slope of a line that goes through (0,0) and shares a point with a circle with center $(2,0)$ and radius $\sqrt{3}$ . This is just the tangent line to the circle that goes through the origins, i.e 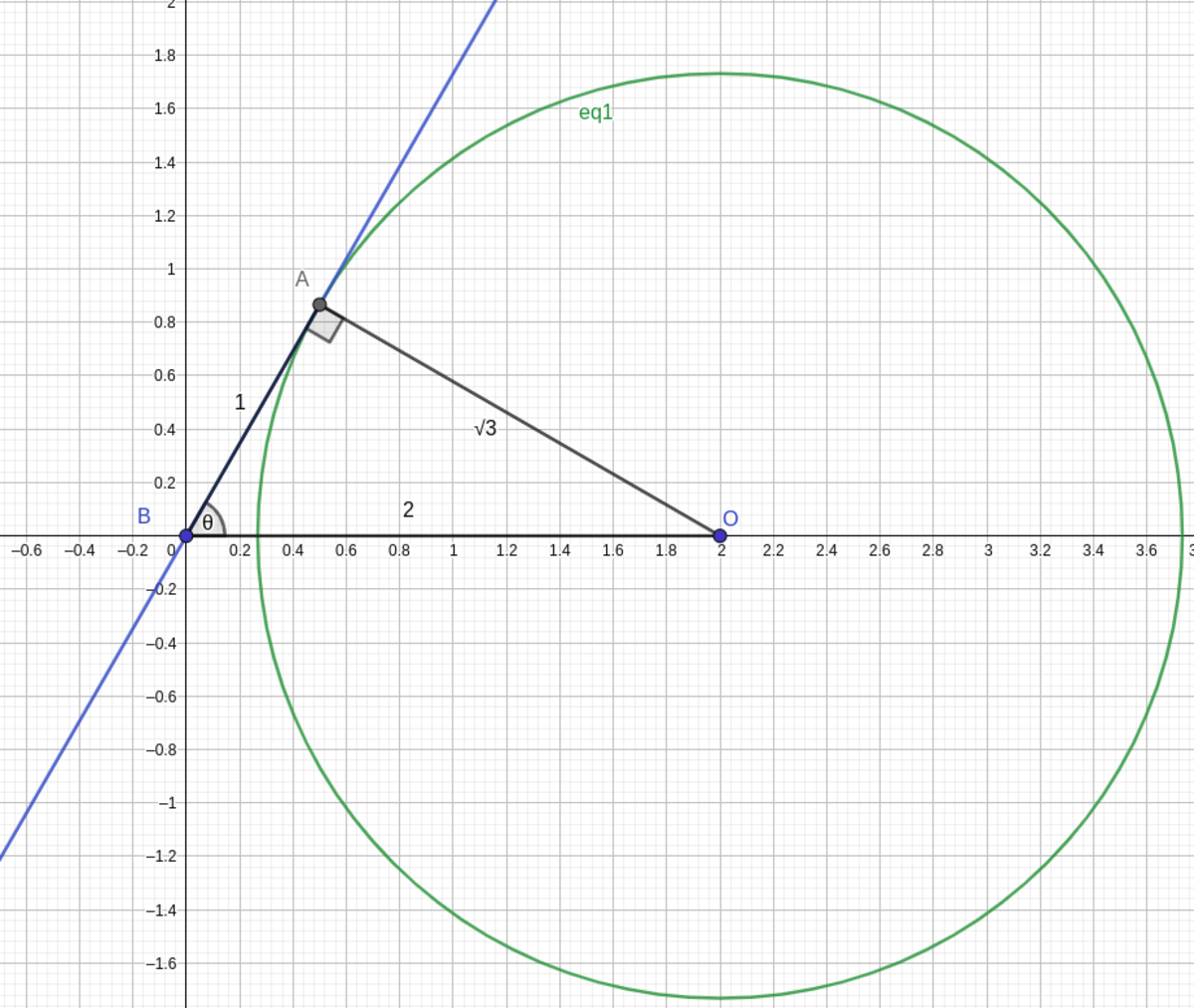Using the right triangle we can figure out the slope, $\tan(\theta) = \sqrt{3}$ . this means the answer is $\left(\sqrt{3}\right)^2 = \boxed{3}$