Piecewise Circle Moment
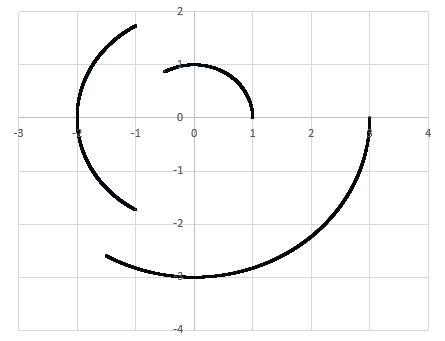
A piecewise circle has the following definition:
x = r cos ( θ ) y = r sin ( θ )
r = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 , 0 ≤ θ ≤ 3 2 π 2 , 3 2 π < θ ≤ 3 4 π 3 , 3 4 π < θ < 2 π
The object has a total mass M which is uniformly distributed as a function of arc length.
If its moment of inertia with respect to an axis perpendicular to the x y plane and passing through ( 0 , 0 ) can be expressed as α M , determine the value of α .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As the mass is uniformly distributed from the origin ( 0 , 0 ) , the arcs can be considered as point masses with masses M 1 , M 2 and M 3 respectively and M 1 + M 2 + M 3 = M . The mass of an arc is proportional to its length. Let the density per length be σ , then we have:
M 1 M 2 M 3 = σ r 1 θ 1 = 1 ( 3 2 π − 0 ) σ = 3 2 π σ = σ r 2 θ 2 = 2 ( 3 4 π − 3 2 π ) σ = 3 4 π σ = σ r 3 θ 3 = 3 ( 2 − 3 4 π ) σ = 2 π σ
⟹ M M 1 M 2 M 3 = M 1 + M 2 + M 3 = ( 3 2 + 3 4 + 2 ) π σ = 4 π σ = 6 1 M = 3 1 M = 2 1 M
The moment of inertia of the object is thus given by:
I = k = 1 ∑ 3 r k 2 M k = r 1 2 M 1 + r 2 2 M 2 + r 3 2 M 3 = 6 1 2 M + 3 2 2 M + 2 3 2 M = 6 M
⟹ α = 6