Piecewise Functions - 7
f ( x ) = ⎩ ⎪ ⎨ ⎪ ⎧ x 4 + 6 x 3 − 5 x 2 − 4 2 x + 4 0 2 π x + sin x if x ≤ a if x > a
Let a function f : R → R be defined as above. As a varies over all real numbers, the maximum number of distinct real roots of f ( x ) = 0 are N .
Let a 1 , a 2 , a 3 , … a n be the integer values of a for which f ( x ) = 0 has N distinct real roots.
Evaluate i = 1 ∑ n a i .
Note: If you think there are no values of a satisfying the conditions, enter your answer as 999.
This problem is part of the set - Piecewise-defined Functions
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you please explain that conclusion of roots :-|
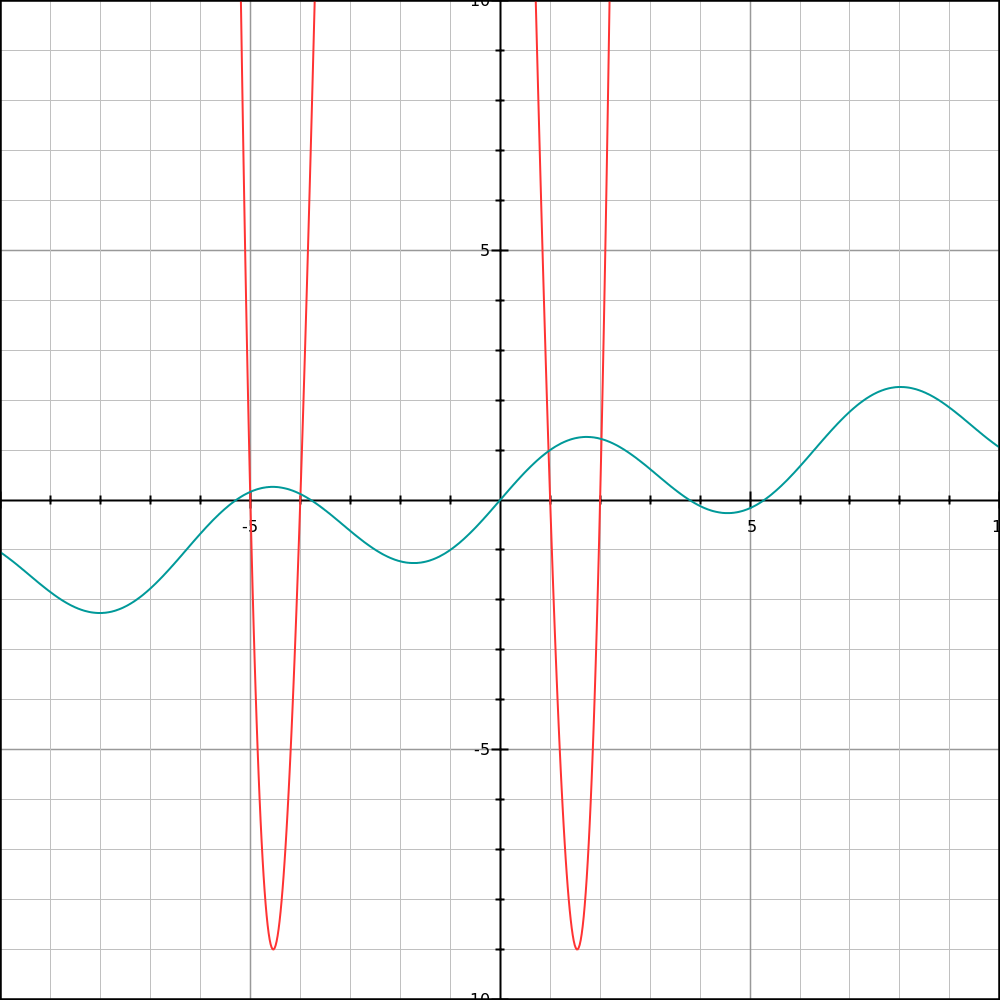
Roughly speaking, since you're looking to have the maximal number of roots, you need the most roots "on the left" plus "on the right".
As you can might be able to see from the graph, this can be achieved by setting a in between the zeroes of the red graph x 4 + 6 x 3 − 5 x 2 − 4 2 x + 4 0 to the left and the zeroes of the blue graph 2 π x + sin x to the right.
This will give us N = 6 ; the integral values of a are then − 4 , 2 , and 3 .
These values are unique; setting a → + ∞ gives N = 4 < 6 ; a → − ∞ yields N = 5 < 6 .
Thus, our answer is − 4 + 2 + 3 = 1 .
(Note: This is by no means a rigorous solution.)
We see that x 4 + 6 x 3 − 5 x 2 − 4 2 x + 4 0 can be factorized as ( x + 5 ) ( x + 4 ) ( x − 1 ) ( x − 2 ) . It will be zero when x = − 5 , − 4 , 1 , 2 .
To find the roots of 2 π x + sin x , we can use numerical methods, to get positive roots as 3 . 7 8 9 . . . and 5 . 2 8 4 . . . . Since it is an odd function, we know that − 3 . 7 8 9 . . . and − 5 . 2 8 4 . . . are its roots as well. x = 0 is also a solution.
We plot these roots (roughly) on the number line (in ascending order). Let's label the roots as A, B , C ... (in ascending order). Also, let the roots of the polynomial be blue and the roots of the other expression be in red.
Then, as we move a from − ∞ to + ∞ , the number of real roots of f will be equal to the number of blue roots to the left of a + number of red roots to the right of a .
Note that the number of real roots of f ( x ) = 0 will be constant in each interval.
Interval ( − ∞ , A ) [ A , B ) [ B , C ) [ C , D ) [ D , E ) [ E , F ) [ F , G ) [ G , H ) [ H , I ) [ I , ∞ ) No. of real roots of f ( x ) = 0 0 + 5 = 5 0 + 4 = 4 1 + 4 = 5 2 + 4 = 6 2 + 3 = 5 2 + 2 = 4 3 + 2 = 5 4 + 2 = 6 4 + 1 = 5 4 + 0 = 4
We see that the maximum possible number of roots are N = 6 , and occur in the intervals [ − 4 , − 3 . 7 8 9 ) and [ 2 , 3 . 7 8 9 ) . The integers in these intervals are − 4 , 2 , and 3 . Thus the integral values of a satisfying the condition are − 4 , 2 , and 3 .
Hence, ∑ a i = − 4 + 2 + 3 = 1 □