Pierino and the Riddle of the Papyrus

Geometry Level 2

Pierino, a well-known character of Italian short stories, has never been a math-enthusiast in his educational career... But he has decided to change his attitude, and he wants to impress his Math teacher at school. He wants to do something that has never done before: solve a puzzle that was found on an ancient Egyptian papyrus...

Here is the riddle.

"An L-sided square is inscribed in a circumference:

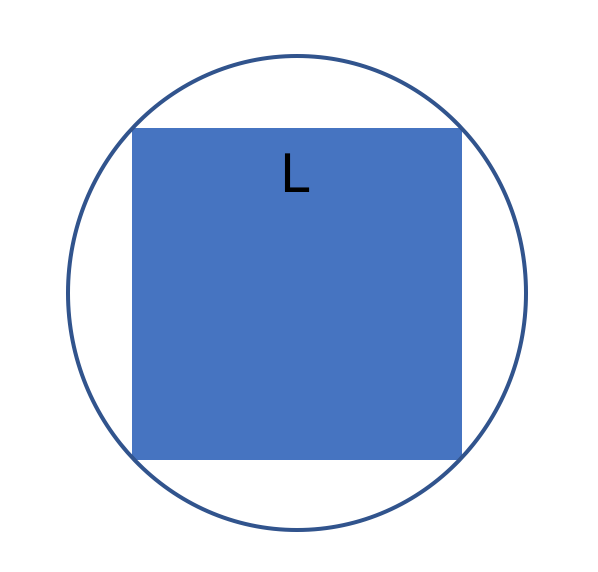
Given the following geometric construction:

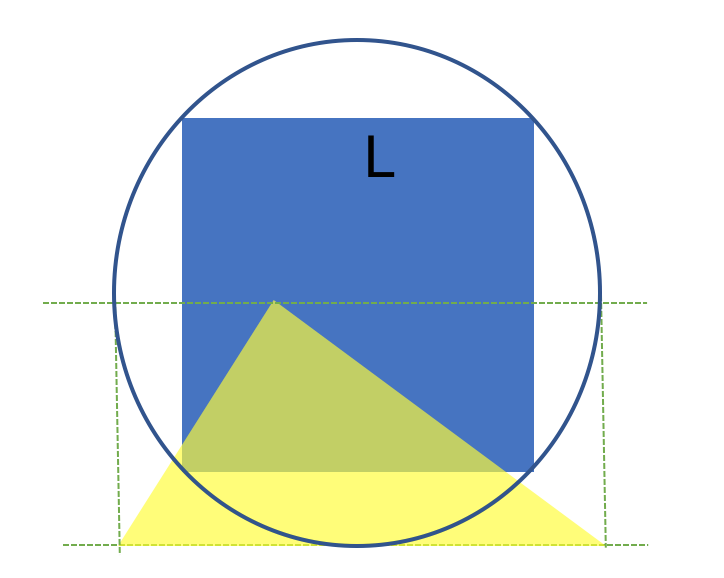
the area of the yellow triangle is... "

Pierino is pretty sure about the answer, but he does not want to miss this opportunity to impress his school teacher, so he is going to give you (the only math freak that he knows) a call in a minute, sort of "Phone-a-friend" lifeline from the Millionaire ... Will you be able to help him?

a quarter of the area of the blue square 2/3 x (the area of the blue square) half of the area of the blue square 3/4 x (the area of the blue square)

Riccardo Della Martera by Riccardo Della Martera , 44, Italy

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

The diameter of the circumference is 2 × L \sqrt{2} \times\ L , which is also the base of the triangle. Thus the area of the triangle is L 2 2 \frac{L^{2}}{2}

5 Helpful 0 Interesting 0 Brilliant 0 Confused
Jeremy Galvagni
Jul 2, 2018

Rotate the square by 45 degrees. The green dotted line then bisects the square into two equal triangles. Each has the same base and height as the yellow triangle. So the yellow triangle's area is half the square.

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Giovanni Delta
Nov 14, 2018

The base of the triangle it's long as the diagonal of the square. The radius of the circumference is an half of the diagonal of the square and is long as the height of the triangle.

So, if we take 1 as the value of L, the base of the triangle (now T ) is 2 \sqrt{2} , and the height of T is 2 2 \frac{\sqrt{2}}{2} . So the area of T is 2 × 2 2 2 \frac{\sqrt{2} \times \frac{\sqrt{2}}{2}}{2} = 2 2 4 \frac{\sqrt{2}^{2}}{4} = 1 2 \frac{1}{2} .

And the area of the square is, of course, 1.

It's the same for every value of L. So the area of T is half of the square area.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...