Pile them up
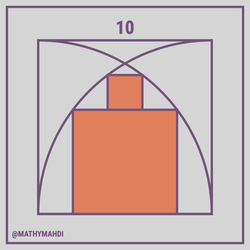 Two quarter circles are inscribed in a square with side length
1
0
. Two more squares are drawn such that they touch the two quarter circles. What is the total area of the two orange squares?
Two quarter circles are inscribed in a square with side length
1
0
. Two more squares are drawn such that they touch the two quarter circles. What is the total area of the two orange squares?
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
If we insert another square just above the square with dimension of 2 and touching the two quadrants, what will its dimensions be? .. It will be 2/3.
Log in to reply
No, why don't you work it out?
Isn't it (8√31 – 42) / 5 ≈ 0.508423? Can the sides actually have a fixed ratio logically?
I have added a general solution.
Log in to reply
Weel generalized! I would have continued to stack all squares, but it doesn't give a clean answer and might get too difficult than the original idea I had in mind.
Let a be the side of the larger orange square and b the side of the small orange square, and place the whole diagram on a Cartesian graph so that the bottom center of the large square is at the origin.
Then the equation of the quarter circle with its center on the left side has an equation of ( x + 5 ) 2 + y 2 = 1 0 0 .
The top right corner of the larger orange square is at ( 2 1 a , a ) , so ( 2 1 a + 5 ) 2 + a 2 = 1 0 0 , which solves to a = 6 for a > 0 .
The top right corner of the smaller orange square is at ( 2 1 b , a + b ) = ( 2 1 b , b + 6 ) , so ( 2 1 b + 5 ) 2 + ( b + 6 ) 2 = 1 0 0 , which solves to b = 2 for b > 0 .
Therefore, the total area of the two orange squares is A = a 2 + b 2 = 6 2 + 2 2 = 4 0 .
Due to symmetry, both of the orange squares would have to be horizontally centered in the middle of the diagram (since the two centers are at the bottom vertices on their left and right each).
If we denote the 2 shorter lines that make up the common radius of the quarters together with the larger orange square's base as x each, then
10² = (10 – x)² + (10 – 2x)²
100 = 5x² – 60x + 200
0 = x² – 12x + 20
= (x – 2)(x – 10)
Since 0 < x < 10,
x = 2
for an area of big square of
= (10 – 2x)² = (10 – 2 × 2)² = 36
Now, with a small square with sides of 2y, we have an equation of
10² = (10/2 + y)² + (10 – 2×2 + 2y)²
= (5 + y)² + (6 + 2y)²
100 = 5y² + 34y + 61
0 = 5y² + 34y – 39
= (5y + 39)(y – 1)
Again, since y > 0,
y = 1
for an area of small square of
= (2y)² = (2 × 1)² = 2² = 4
Answer = 36 + 4 = 40
Let r = 1 0 . For both red squares with sides h 1 , h 2 , we can find a right triangle containing its top-left corner, and the bottom-right corner of the entire figure: h 1 : h 2 : r 2 r 2 = h 1 2 + ( 2 r + 2 h 1 ) 2 = ( h 1 + h 2 ) 2 + ( 2 r + 2 h 2 ) 2 ⇒ ⇒ h 1 2 + 5 2 r h 1 − 5 3 r 2 h 2 2 + 2 5 3 4 r h 1 − 1 2 5 3 9 r 2 = 0 = 0 ⇒ ⇒ h 1 h 2 = 5 − 1 ± 4 r = 2 5 − 1 7 ± 2 2 r ⇒ ⇒ h 1 h 2 = 5 3 r = 5 r The total read area is h 1 2 + h 2 2 = 5 2 r 2 = 4 0
Label the three squares as A B C D , E F G H , and I J K L as shown. Let the side lengths of square E F G H and square I J K L be a and b respectively, and K M be perpendicular to A B . By Pythagorean theorem ,
A F 2 + F G 2 ( A E + E F ) 2 + F G 2 ( 2 1 0 − a + a ) 2 + a 2 5 a 2 + 2 0 a − 3 0 0 a 2 + 4 a − 6 0 ( a − 6 ) ( a + 1 0 ) ⟹ a = A G 2 = A G 2 = 1 0 2 = 0 = 0 = 0 = 6 Since a > 0
Similarly,
A M 2 + K M 2 ( A F − M F ) 2 + ( K J + J M ) 2 ( 8 − 2 6 − b ) 2 + ( b + 6 ) 2 5 b 2 + 6 8 b − 1 5 6 ( 5 b + 7 8 ) ( b − 2 ) ⟹ b = A K 2 = A K 2 = 1 0 2 = 0 = 0 = 2 Since b > 0
The sum of areas of square E F G H and square I J K L is a 2 + b 2 = 6 2 + 2 2 = 4 0 .
Generalization: Answering questions by @Vijay Simha and @Saya Suka .
Let the side length of the n th stacked square be a n . Then a n is given by:
( 5 + 2 a n ) 2 + ( a 1 + a 2 + a 3 + ⋯ + a n ) 2 = 1 0 2
And we have:
n = 1 : n = 2 : n = 3 : n = 4 : ⋯ ( 5 + 2 a 1 ) 2 + a 1 2 = 1 0 0 ( 5 + 2 a 2 ) 2 + ( 6 + a 2 ) 2 = 1 0 0 ( 5 + 2 a 3 ) 2 + ( 8 + a 3 ) 2 = 1 0 0 ( 5 + 2 a 4 ) 2 + ( 5 8 3 1 − 2 + a 4 ) 2 = 1 0 0 ⟹ a 1 = 6 ⟹ a 2 = 2 ⟹ a 3 = 5 8 3 1 − 4 2 ⟹ a 4 = 5 4 1 9 5 3 + 2 0 8 3 1 − 3 2 3 1 − 4 2