A geometry problem by Aziz Alasha

**Fist of all connect the points A and C by a straight line ,Then bythe similarity of the two triangles ;

(7 – f) / 9 = f /14 , f = 98/23 , 7- f = 63/23 .The fore ; using the pitagorian theorem , we get

L1² = 9² + (9*7/23)²

L2² = 14² + (14*7/23)²

L1 +L2 = √578 = 17√2 = a√2

a = 17 **

---

we can add an other different solution :

As shown on the figure ; extend the line NM to intersect the line AB at E

Angle MAB = Angle DCN = α

Angle MEA = 90 - α

Let the Co-ordinates of A = (0,0) , then ;

M = (14cos α , 14sin α)

N = (14cos α – 7sin α , 14sin α + 7 cos α )

C = (23cos α – 7sin α , 23sin α + 7 cos α )

Then

AC² = (23cos α – 7sin α )² + ( 23sin α + 7cos α)²

AC ² = 578

AC = √578 = 17√2 = a√2

a = 17

---

Note as the slope of AC = 1 , then it can be shown that the x and y coordinate of C are equal , hence tan α = $\frac{8}{15}$

and sin α = $\frac{8}{23}$ , cos α = $\frac{15}{23}$

substittuting we get the same answer.

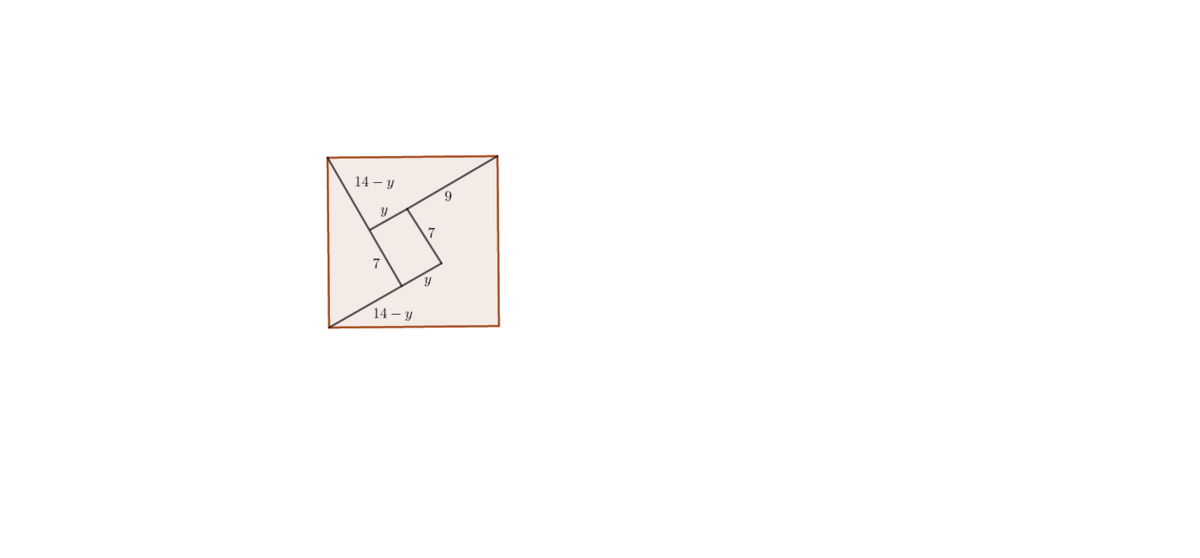
Here's a different approach. Extend the lines as shown and use the rectangle and congruent right triangles to label the indicated lengths. It now follows that 7 + (14 - y) = y + 9, or equivalently y = 6. Thus the right triangles have legs of length 8 and 15. Now use the Pythagorean Theorem to find the side of the square is 17.

This solution was fairly easy to visualize. Using black lines, extend the original blue lines to create the center rectangle with dimensions of 5 x 7 units. The green lines show an expansion of the rectangle into a 7 x 7 square. By definition, this results in the four congruent outer triangles with sides of 8, 15, and 17.

(Sadly I do not know how to include a picture in my solution) | Extend the line which starts with length 14 so that the EXTENSION is 9. And then add the line that ends at the opposite diagonal which will be perpendicular to the other line starting with length 14 and extending by 9. (The point after the extension will be outside the square). So by Pythagoras, and calling the diagonal of the square D, D^2 = 23^2 + 7^2 = 529 + 49 = 578. DO NOT TAKE THE SQUARE-ROOT TO FIND THE DIAGONAL. Because then the Pythagoras theorem can be used again, calling L the length of the square. And you get 2 x L^2 = D^2. And we have just found D^2 to be 578. So 2 x L^2 = 578. So L^2 = 289. So L = 17. Regards, David Ps My poor attempt at a diagram is the best that I can do (though I realize when I look at it that it has not been accepted by the computer!). abcd is the square. This has Diagonal D and side length L. And X is the point which is 23 away from point d and 9 away from point b.

a _ _ _ _ _ b | | | | | | | | X | | | | | _ _ _ __ | d c