Pi>Tau

Geometry Level 1

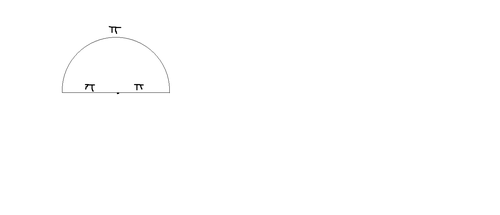Kirk claims that he has developed a proof that pi's numerical value is greater than tau:
(1) Take a semicircle of radius pi.
(2) The diameter is two pi and the semi-circumference is pi.
(3) The semi-circumference is an inflation of the diameter which is two pi, also known as Tau.
(4) Obviously, the semi-circumference is greater than the diameter.
(5) Pi's numerical value is greater than tau in circles with radius pi.

Spock comes along and picks one of the steps above that is illogical. Which is it?


The answer is 2.

Spock Weakhypercharge by Spock Weakhypercharge , 96, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

The semi-circumference is pi squared.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

given semicircle's perimeter is 3pi . According to formula it is pi(pi + 2). so 2 is wrong

0 Helpful 0 Interesting 0 Brilliant 0 Confused

If radius is pi then the semi circumference would be 1/2 of pi^3

0 Helpful 0 Interesting 0 Brilliant 0 Confused

No diameter is 2pi not pi ^2

Chamelean Brown - 7 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...