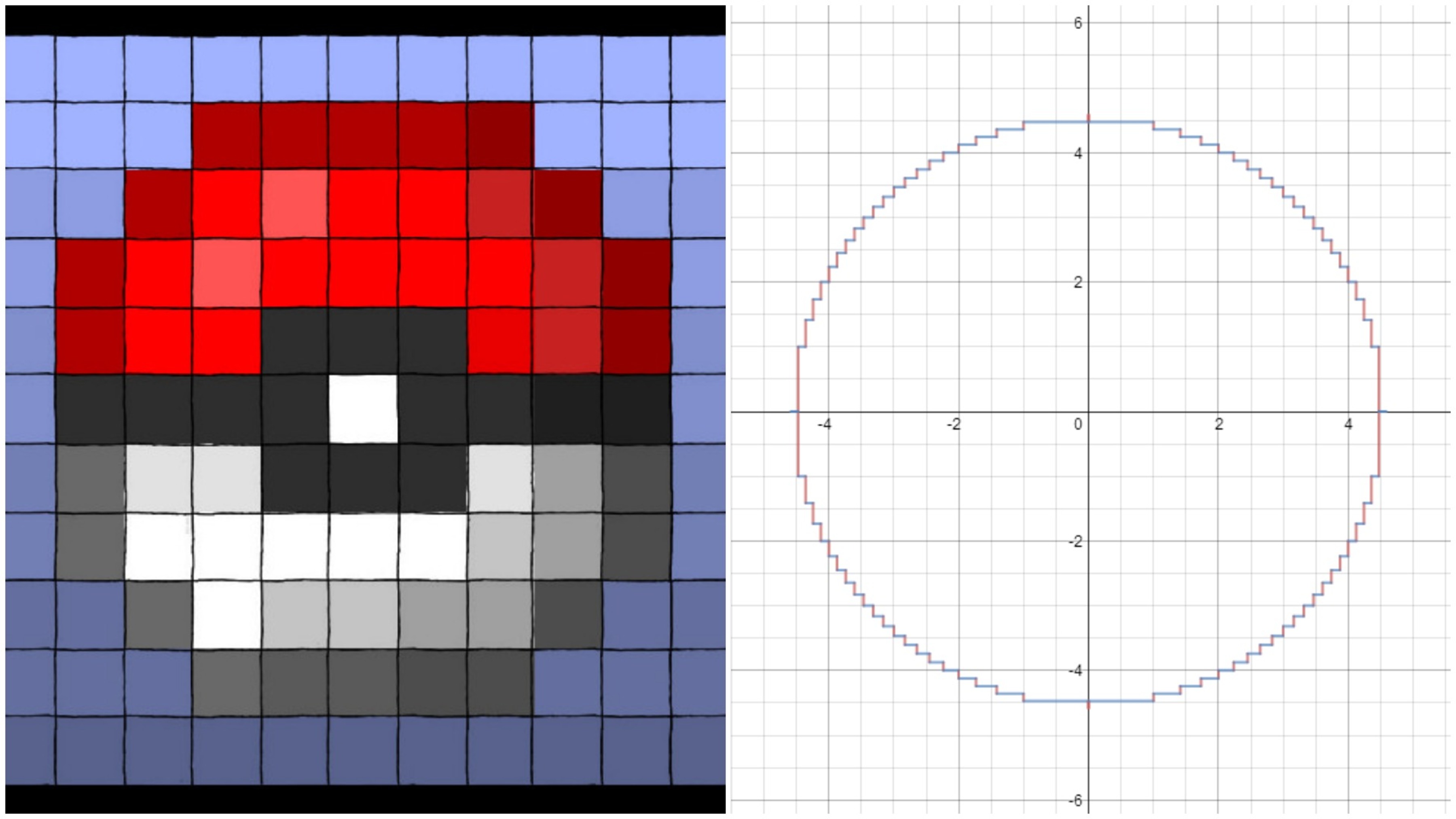
Pixelated Poké Ball

Excellent question! Loved the pokemon Red, Blue, Yellow and Green reference. Hope you don't mind me adding this awesome problem to the set Mathematics in Anime .

Solution (A rough sketch, not very rigorous but can be easily generalized):

Since the "curve" is symmetrical, it suffices to evaluate $\displaystyle \int_{0}^{\sqrt{20}} y dx=\displaystyle \int_{0}^{\sqrt{20}} \sqrt{20-\left\lfloor x^{2} \right\rfloor}dx$ before multiplying it by $4$ .

Write $x=d+e$ , where $d$ is the integer part of $x$ while $e$ is the fractional part. Divide into $5$ cases, where $d=0,1,2,3,4$ .

We have $\displaystyle \int_{0}^{\sqrt{20}} \sqrt{20-\left\lfloor x^{2} \right\rfloor} dx=$

$\displaystyle \int_{0}^{1} \sqrt{20} de + \displaystyle \int_{0}^{1} \sqrt{19-\left\lfloor e^{2}+2e \right\rfloor} de+ \displaystyle \int_{0}^{1} \sqrt{16-\left\lfloor e^{2}+4e \right\rfloor} de + \displaystyle \int_{0}^{1} \sqrt{11-\left\lfloor e^{2}+6e \right\rfloor} de+ \displaystyle \int_{0}^{\sqrt{20}-4} \sqrt{4-\left\lfloor e^{2}-8e \right\rfloor} de$ .

However, this whole mess is still not integrable directly. To find a way around this, I will illustrate using the case $\displaystyle \int_{0}^{1} \sqrt{19-\left\lfloor e^{2}+2e \right\rfloor} de$ .

Denote $f(e)=e^{2}+2e$ . It is obvious that the range of $f(e)$ for $0 \leq e <1$ is $[0,3)$ . When $f(e)=0$ , $e=0$ . Similarly, solving for $f(e)=1$ , we get $e=\sqrt{2}-1$ . For $f(e)=2$ , we get $e=\sqrt{3}-1$ , and for $f(e)=3$ , we get $e=1=\sqrt{4}-1$ .

Rewrite $\displaystyle \int_{0}^{1} \sqrt{19-\left\lfloor e^{2}+2e \right\rfloor} de$ as $\displaystyle \int_{0}^{\sqrt{2}-1} \sqrt{19} de +\displaystyle \int_{\sqrt{2}-1}^{\sqrt{3}-1} \sqrt{18} de+\displaystyle \int_{\sqrt{3}-1}^{\sqrt{4}-1} \sqrt{17} de$ .

The expression equals $\sqrt{19}(\sqrt{2}-1-0)+\sqrt{18}(\sqrt{3}-1-\sqrt{2}+1)+\sqrt{17}(\sqrt{4}-1-\sqrt{3}+1)$ .

Rewriting this into the desired form, we find it equals $\sqrt{19}(\sqrt{2}-\sqrt{1})+\sqrt{18}(\sqrt{3}-\sqrt{2})+\sqrt{17}(\sqrt{4}-\sqrt{3})$ .

Since the remaining cases are analogous and can be proven in this similar manner, this leads to the obvious conjecture that the area equals:

$\displaystyle \sum_{n=1}^{20} 4\sqrt{n}(\sqrt{21-n}-\sqrt{20-n})$ . Therefore, $R=4,Y=20,G=21,B=20$ .

The desired answer follows. $\frac{R.G.B}{Y}=\frac{4.20.21}{20}=\boxed{84}$ .

---

Gotta catch them all! Happy 20th anniversary, everyone! :)

First of all, as shown in the graph, the floor function in the first equation will yield the same number under a certain range, regardless of changes in the domain value. For instance, the domain must stay at a fixed value of $\sqrt { 20 }$ under the range $[ 0 , 1 )$ . Conversely, the floor function in the second equation will yield the same number under a certain domain, regardless of changes in the range value. In its case, the range must remain at $1$ under the domain $[ \sqrt { 19 } , \sqrt { 20 } )$ .

Therefore, the resultant figure will look like a series of steps, with the first equation forming vertical lines and the second equation forming horizontal lines. From here, one can take a geometric approach, similar to a Riemann sum, in which one calculates the area of the first quadrant by summing all of the rectangular slices formed under all the steps. One can do this with the slices stacked horizontally or vertically , but in this case, I will show you how to do it vertically , with intervals defined by $x$ .

This can be done by noticing how the heights of each rectangle vary, as according to the first equation, under intervals of $\sqrt { k }$ , where $k$ is an integer. From here, one can make a table, which lists the length, height, and area of each of these rectangles:

I have truncated this table, since after only a few terms, one can see the pattern which emerges. By adding up each of these individual areas for the rectangular slices, one can represent the area of the figure in the first quadrant: $\displaystyle \sum_{n=1}^{20} \sqrt{n}(\sqrt{21-n}-\sqrt{20-n})$ Since the figure is equally divided between all quadrants, this sum multiplied by 4 will give an expression for the area of the entire figure in all quadrants: $\displaystyle \sum_{n=1}^{20} 4\sqrt{n}(\sqrt{21-n}-\sqrt{20-n})$

From here, the answer is $\frac { RGB }{ Y } =\frac { 4\cdot 20\cdot 21 }{ 20 } =\boxed { 84 }$ .