Pizza Cutting Puzzle!

Geometry Level 5

A 12 inch diameter round pizza

has been sliced by 3 straight cuts, leaving a right triangle in the middle as shown here

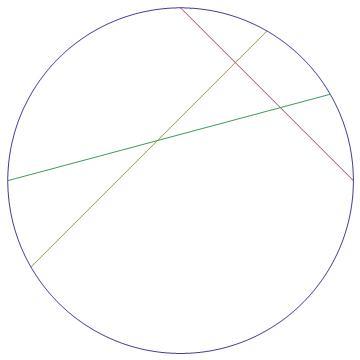
The edge of the pizza has been cut into 6 arcs, one each of the following, in degrees, totaling 360 degrees:

${15, 30, 45, 60, 90, 120}$

but not necessarily in that order. The maximum area, in square inches, this right triangle piece in the middle can have can be expressed as

$\dfrac { 1 }{ a } (b+c\sqrt { 2 } +d\sqrt { 3 } +e\sqrt { 6 } )$

where $a, b, c, d, e$ are integers (which may be negative). Find $a+b+c+d+e$ .

Integer $a$ is positive. Do not rely on diagram to guess arcs in degrees.

The answer is 58.

1 solution

Michael Mendrin
Jul 11, 2014

The exact maximum area is

$\dfrac { 1 }{ 4 } (72-45\sqrt { 2 } +60\sqrt { 3 } -33\sqrt { 6 } )$

obtained by cutting the pizza into arcs in the following order

$30,45,60,90,15,120$

Hence, $4+72-45+60-33=58$

To simplify search for maximum right triangle, note that $2$ perpendicular chords in a circle divide the edge into $4$ arcs such that opposite arcs always add up to $180$ degrees. Then you could almost infer the optimum order of arcs by sketching on paper.

Pizza Cutting Puzzle!

The answer is 58.

1 solution

0 pending reports