Pizza Slicing Time!
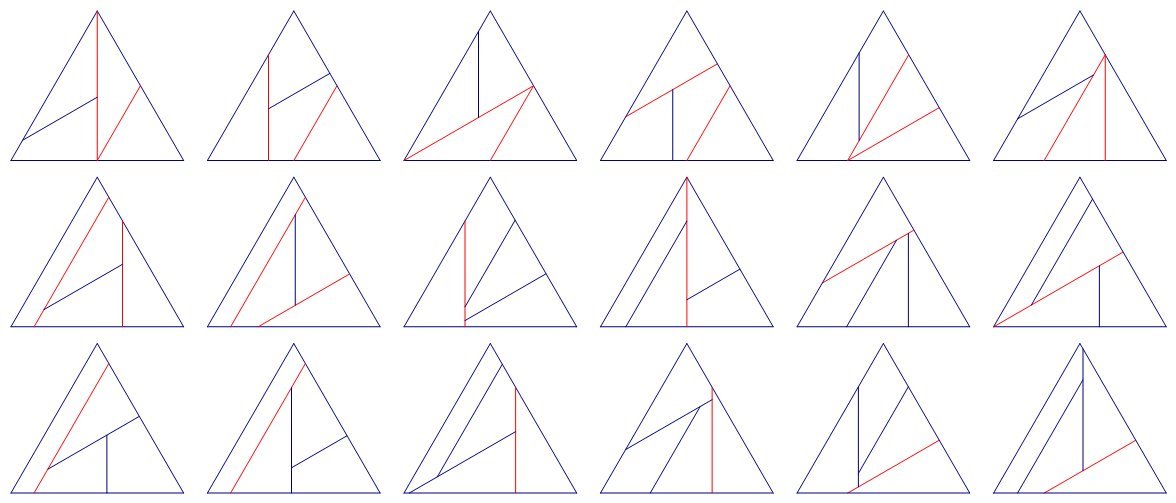
Mr. Lefty plans to cut an equilateral-triangle-shaped pizza into four parts of congruent areas. He does this with three cuts made at angles 3 0 ∘ , 6 0 ∘ , and 9 0 ∘ , each measured counterclockwise from the horizontal. The diagram below shows two examples of how the pizza may be cut.
The dashed lines are there to show how the cuts not touching the horizontal segment are made.
In total, how many ways are there to cut the pizza (including the two ways shown above)?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
There are a full 1 8 possible set of cut shapes. If you look at my diagram, the first six shapes can each be cut out in three orders, the next six can also each be cut out in two orders, and the last six can only be cut out in one order. Thus there are a total of 3 6 cutting orders which could result in a quartered pizza.
Though if we have to include the two examples then the answer is only three because the only other correct answer is to not cut it because if you are unfortunate to end up in this scenario where you have a equilateral triangle pizza and people are trying to cut it up in inefficient ways then you don't cut it and tell them to fend for themselves as you curse their overcomplicating of a simple problem.
There are a total of 1 8 possible arrangements of slices. Eight of these involve two "crust-to-crust" slices, and can be found by simply considering which pairs of "crust-to-crust" slices are possible. The next four involve just one "crust-to-crust" slice, with two more slices from the crust to the cut formed by the first slice. The last six have just one "crust-to-crust" slice, one cut joining the crust to the cut formed by the second slice, and the third cut joining the crust to the cut formed by the second slice. These last ten can all be found by systematically running though the nine possible "crust-to-crust" slices and seeing which permit a dissection that does not contain a second "crust-to-crust" slice. In the diagram below the "crust-to-crust" slices are shown in red.
How exactly do we show that these are all the possibilities?
Log in to reply
It’s a process of exhaustion. If we have two crust-to-crust cuts, we must have two quarters and a half. There is then only one way to bisect the half.
If we have just one C2C cut, we either have two halves or one quarter and a three-quarter. If two halves, each has to be bisected, and there are at most two ways (discarding any options that introduce a second C2C cut) ways of doing this. Otherwise we have to trisect the remaining piece. This has to be done by cutting off a third of it, and bisecting the remainder. There are at most 4 ways of cutting off a third (two cut directions, and deciding “which end” to cut the third from), and then only one way to bisect the remaining piece. Again, we must ignore choices that produce a second C2C slice. Just check all the options...
Let's denote A X ( n ) to be the combination of cuts beginning with a cut of X ∗ enclosing 4 n of the triangle on it's left hand side. E.g The examples above lie within ( A 9 0 ( 1 ) and A 6 0 ( 3 ) ) and ( A 9 0 ( 2 ) and A 6 0 ( 3 ) ) respectively.
Also, for an area of 4 3 the original, denote B X ( n ) to be the combination formed from a cut of X ∗ enclosing 3 n of the shape on it's left hand side, followed by the remaining cut, cutting the final piece in half.
∣ A 9 0 ( 1 ) ∣ can be seen to be 2, as B 3 0 ( 1 ) = B 6 0 ( 2 ) , B 3 0 ( 2 ) = B 6 0 ( 1 ) . ∣ A 9 0 ( 2 ) ∣ = 2, as you can either assign the 3 0 ∗ cut to the left or right half. ∣ A 9 0 ( 3 ) ∣ = 4, as B 3 0 ( 1 ) , B 6 0 ( 2 ) , B 3 0 ( 2 ) , B 6 0 ( 1 ) are all unique. By rotating the triangle 6 0 ∗ , one can see that ∣ A 3 0 ( n ) ∣ = ∣ A 9 0 ( 4 − n ) ∣ .
Observing the previous cut combinations included. One can note that all the combinations within A 6 0 ( 2 ) are already included in A 3 0 ( 3 ) and A 9 0 ( 3 ) . Also, those in A 6 0 ( 3 ) are all already present (Combinations where either the 3 0 ∗ or 9 0 ∗ cut touch 2 edges of the original triangle are already counted).
For A 6 0 ( 1 ) , B 3 0 ( 2 ) and B 9 0 ( 2 ) can be seen in A 3 0 ( 3 ) and A 9 0 ( 3 ) respectively, but B 3 0 ( 1 ) and B 9 0 ( 1 ) are unique.
This sums to 8+8+2=18 total.
- Some maths can be done to work out if cuts meet another cut or not. Mostly it will appear quite obvious, but notably when performing the first cut of A 9 0 ( 1 ) and A 3 0 ( 3 ) , these leave a small triangle of area 4 1 of the original. The edges of this triangle shared with the original are 2 L and 2 2 L , and 2 2 3 L ≈ 1 . 1 L > L
It doesn't matter which slice is which.
Choose the first slice. It can be made in any of 3 ways. 1/4 of the way, 1/2 way, or 3/4 of the way.
If the first was made at the 1/4 mark, there are two choices for slicing the remaining 3/4 into thirds.
If the first was made at 1/2 way, there are two choices for which to slice into the other halves.
If the first was made at the 3/4 mark, there are again two more choices.
Total 3 ⋅ 3 ⋅ 2 = 1 8
Note: some of the choices do lead to identical pieces at the end, but the question is how many ways there are to cut the pizza.