Placing Numbers in a Square 2
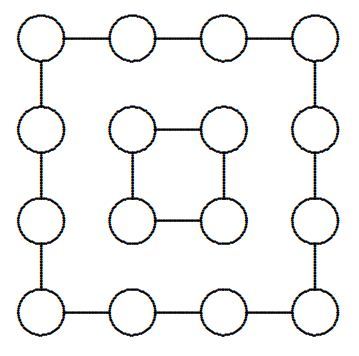 Each of the integers from 1 to 16 is to be placed once each in one of the circles in the figure so that the integers along each of the four outer sides of the large figure and the four integers that make up the inner figure have identical sums. What is the largest sum, if any, that can be obtained?
Each of the integers from 1 to 16 is to be placed once each in one of the circles in the figure so that the integers along each of the four outer sides of the large figure and the four integers that make up the inner figure have identical sums. What is the largest sum, if any, that can be obtained?
If you want to solve it's sister problem, an easy version, try this: Placing Numbers in a Square #1
The answer is 38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I found it rather easy for some reason. Normally I never get level 5 questions.
Several found by computer program:
Thing solved was unlocked status of random.
Answer: 3 8
Define the sum along each side as a . Note that 5 a -corner sum = 1 3 6 , where 1 3 6 = 1 + 2 + . . . 1 6 . We want to maximize a , so that means maximizing the corner sum.
Note that 5 a = 1 3 6 + corner sum ≡ ( 1 + corner sum ) ( m o d 5 ) , implying that corner sum ≡ 4 ( m o d 5 )
The upper bound for the corner sum is 1 3 + 1 4 + 1 5 + 1 6 = 5 8 ≡ 3 ( m o d 5 ) . Wishful thinking compels us to try the highest possible corner sum which is congruent to 4 ( m o d 5 ) , in this case, 5 4 .
As many people have pointed out, there are multiple possible solutions to this puzzle. Mine is as follows: From top right corner, clockwise: 1 3 , 7 , 4 , 1 4 , 8 , 1 , 1 5 , 5 , 6 , 1 2 , 2 , 1 1
In small square: 3 , 9 , 1 0 , 1 6
Moderator note:
For clarity, make sure you define terms when you first use them, and explain exactly what you are thinking. For example, " 5 a -corner sum" might be interpreted as an undefined term, instead of the expression "5a minus the corner sum".
Good approach otherwise.
This is the shortest solution I could come up with. We know that the sum of numbers in all the boxes adds up to 136 because 16*17/2=136. The maximum possible sum of the four outer sides and the inner square will be 194. This is because the corners count twice towards the sum because they fall under two sides and we can get the largest value by putting the largest numbers in the corners i.e. 16, 15, 14 and 13. We get 194 because we add 13, 14, 15 and 16 again to 136. We know that the total sum of the 4 outer sides and the inner square has to be a multiple of 5. We cannot go larger than 194 as the sum as it is the maximum but we can round the number down to 190. Dividing it by 5 we get the maximum sum for each side. Of course there could be smaller numbers, but we have to test this. I decided to put 12, 13, 14 and 15 for the corners and I got this solution:
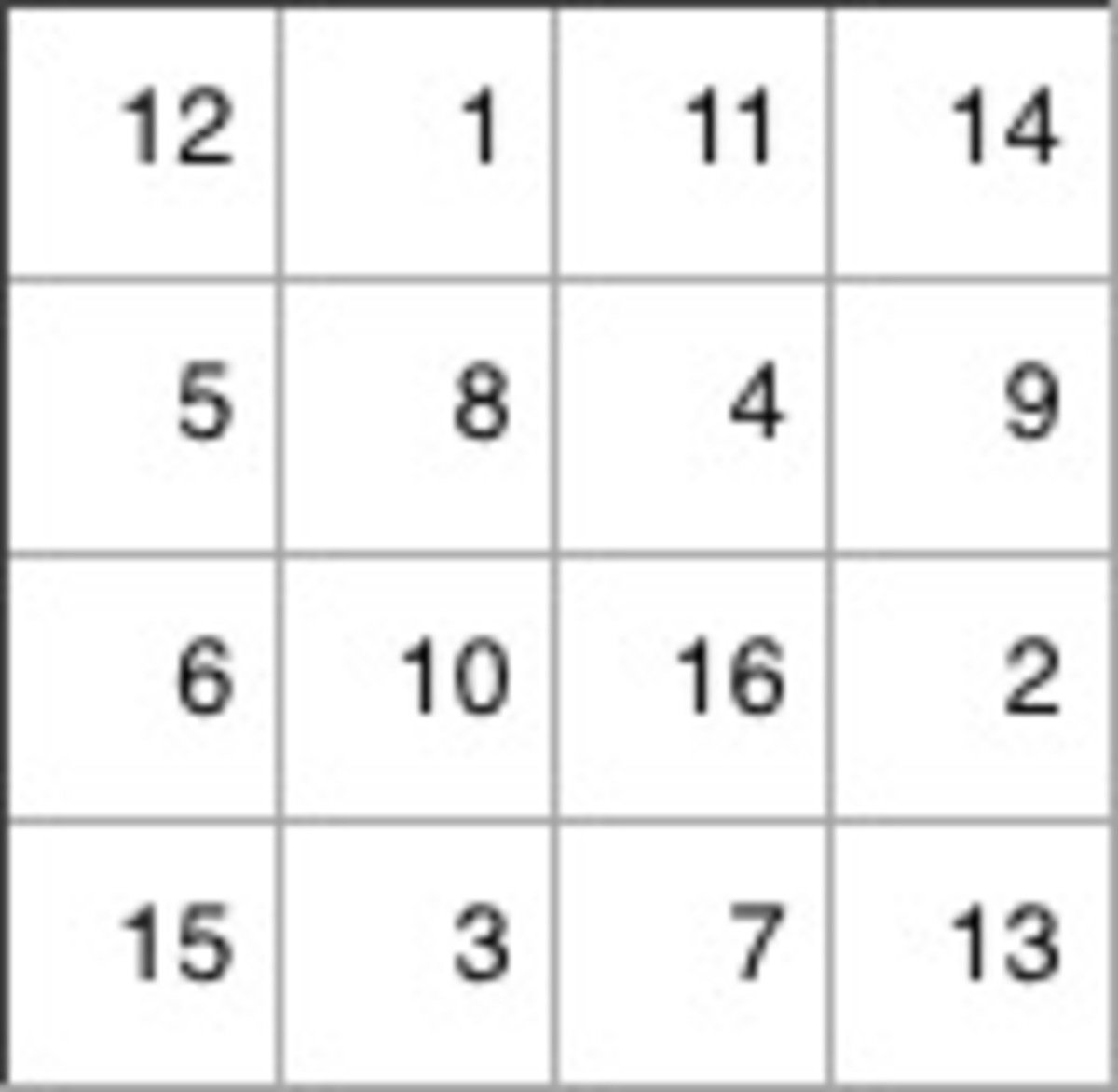
Moderator note:
Good approach with finding the theoretical maximum, and then attempting to achieve it. There are multiple solutions, depending on which set of 4 numbers you choose which sum up to 1 9 0 − 1 3 6 .
You can improve on your solution by formatting it properly. Use line breaks and paragraphs to keep your ideas distinct.
from rightmost top yours no. Will go like this of big square . Clockwise -- 15,10,4,9,3,12,14,1,7,16,2,5 & in small square -11,13,6,8.
This question is a little bit more complex than its sister, and the solution will be significantly longer than its counterparts. The sum to all numbers from 1 to 16 is 2 1 6 × 1 7 = 1 3 6 . Define the upper leftmost of the outer grid as x 1 , for each number on the clockwise order as x 2 , x 3 , … x 1 2 , and the inner grid as x 1 3 , x 1 4 , x 1 5 , x 1 6 . From the condition provided, we will get four equations: x 1 + x 2 + x 3 + x 4 = x 1 3 + x 1 4 + x 1 5 + x 1 6 x 4 + x 5 + x 6 + x 7 = x 1 3 + x 1 4 + x 1 5 + x 1 6 x 7 + x 8 + x 9 + x 1 0 = x 1 3 + x 1 4 + x 1 5 + x 1 6 x 1 0 + x 1 1 + x 1 2 + x 1 = x 1 3 + x 1 4 + x 1 5 + x 1 6 to which I will add the following x 1 3 + x 1 4 + x 1 5 + x 1 6 = x 1 3 + x 1 4 + x 1 5 + x 1 6 Now, once we have five equations, combine them all will gives n = 1 ∑ 1 6 ( x n ) + ( x 1 + x 4 + x 7 + x 1 0 ) = 5 ( x 1 3 + x 1 4 + x 1 5 + x 1 6 ) or simply 1 3 6 + ( x 1 + x 4 + x 7 + x 1 0 ) = 5 ( x 1 3 + x 1 4 + x 1 5 + x 1 6 ) Now, to get the maximum number to the right hand side (which equals to the sum of each side in the outer loop), we will try to replace x n on the left-hand side with the maximum number from 1 to 16 while taking account that all of the value must be integer.
Without prejudicing the general characteristics, we will replace the value of ( x 4 , x 7 , x 1 0 ) = ( 1 6 , 1 5 , 1 4 ) . Here we will get 1 8 1 + x 1 = 5 ( x 1 3 + x 1 4 + x 1 5 + x 1 6 ) . Provided that all number must be integer and the right hand side is a multiple of 5, the maximum number x 1 can be is 9, which resolved to yield x 1 3 + x 1 4 + x 1 5 + x 1 6 = 3 8 as the maximum value possible for the sum in the inner loop and each of the outer loop.
An example where the sum of all rows in the outer loop equals to the sum inside the inner loop, and yield the maximum number of 38 is provided here: Example
Example