Planetary Ballistics
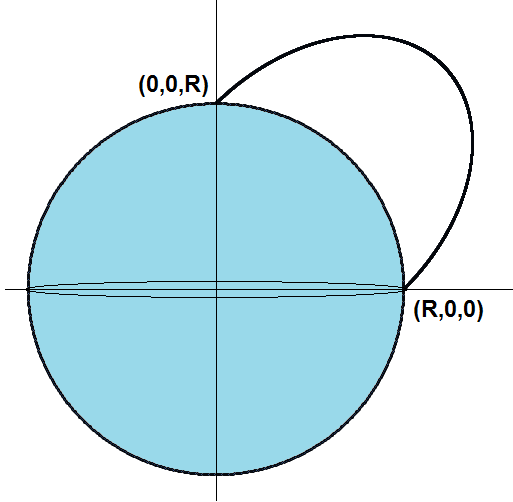
There is a uniform spherical planet of radius with its center at the origin of the coordinate system. A projectile is launched from the "North Pole" at with its initial velocity pointed in the direction of the vector .
Let the escape speed relative to the planet's surface be . With the given launch vector, let the minimum launch speed for the projectile to reach the equatorial point be . The two are related as follows:
Determine the value of
The answer is 0.7071.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The escape velocity is v e = R 2 G M where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet. Since all the particle's motion lies outside the planet's radius, we can assume that the planet's attraction is as from a point particle, and so the equation of motion of the particle is m r ¨ = − r 2 G M m r ^ = − 2 r 2 m R v e 2 r ^ where m is the mass of the projectile. Thus r ¨ = − 2 r 2 R v e 2 r ^
The trajectory of the particle is an ellipse with one focus being the origin. By symmetry, the major axis is along the line y = x . Since the particle's velocity is parallel to the vector ( 1 1 ) at the point of projection, we deduce that the point of projection and the point of collision with the earth are the opposite ends of the minor axis. Thus (in the standard notation) b = a e = 2 1 R , and hence e = 2 1 and a = R .
Using plane polar coordinates as shown in the diagram, standard theory shows that r 1 = R v 0 2 v e 2 ( 1 + e cos θ ) = R α 2 1 ( 1 + 2 1 cos θ ) When θ = 4 3 π we have r = R , and hence α = 2 1 .