Planetary Opposition: Can You Solve It?

Classical Mechanics Level 2

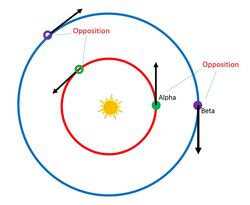Consider two planets of perfectly circular and concentric orbits, orbiting around a star. The orbit of the planet closest to the star (Planet Alpha) has an orbital radius of 100 million kilometers and a constant linear speed of 9,513 m/s. The orbit of the other planet (Planet Beta) has an orbital radius of 200 million kilometers and a constant linear speed of 31,710 m/s. The planets are orbiting in opposite directions. If the planets begin in opposition at time t = 0 t=0 then when is the next time, in years, when the planets will be in opposition again?

Note that the picture above is to only to serve as an example of what an opposition looks like; a given answer may appear to contradict certain elements in the picture. This does not necessarily mean that an answer is incorrect.

Details and Assumptions :

  • The planets' gravitational fields will not interfere with each other
  • An opposition is when two planets are aligned, sharing the same angle.

Hint: convert speeds to kilometers per year.

t ≈ 0.7854 t \approx 0.7854 years t ≈ 0.5236 t \approx 0.5236 years t ≈ 1.571 t \approx 1.571 years t ≈ 2.356 t \approx 2.356 years

Jason Simmons by Jason Simmons , 26, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jason Simmons
Dec 1, 2015

First, we convert each linear speed from m/s to km/yr as suggested by the hint. With this, we find that the linear speed of Planet Alpha is 300 million km/year and the linear speed of Planet Beta is 1,000 million km/yr. Because the planets exhibit circular motion we will convert the linear speeds to angular velocities using a familiar formula from physics.

ω = v r \omega= \frac{v}{r}

From here we can determine that the angular velocity of Planet Alpha is 3 rad/yr and the angular velocity of Planet Beta is 5 rad/yr. It follows that

ω = θ t ⇒ θ = ω t \omega= \frac{ \theta}{t} \Rightarrow \theta = \omega t

and since we have a value for theta in terms of time, we can now find the y-components of each planet at time t t using

y = sin ⁡ ( θ ) = sin ⁡ ( ω t ) y=\sin(\theta)=\sin(\omega t)

So now we have two equations:

y α = sin ⁡ ( 3 t ) y_{\alpha}=\sin(3t) and y β = − sin ⁡ ( 5 t ) y_{\beta}=-\sin(5t)

and we want to find when these two equations are equal to each other. In this case, we want to find the very first instance for when each y-component is a minimum. Solving for t t we find that

t = π ( n + 1 2 ) t=\pi(n+ \frac{1}{2}) and our zeroth instance occurs at n = 0 n=0 which gives that

t = π 2 ≈ 1.571 years \boxed{t=\frac{\pi}{2} \approx 1.571\: \textrm{years}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

The reason you have one solver is because the answer is incorrect. In your solution you have mistakenly converted to 5 rad/yr while it is in fact 5000 rad/yr for planet beta. Same for planet alpha. The real solution should be 0.003142 years or 1.1467 earth days.

William G. - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...