Ptolemy's Theorem but it's related rates :)

Calculus Level 2

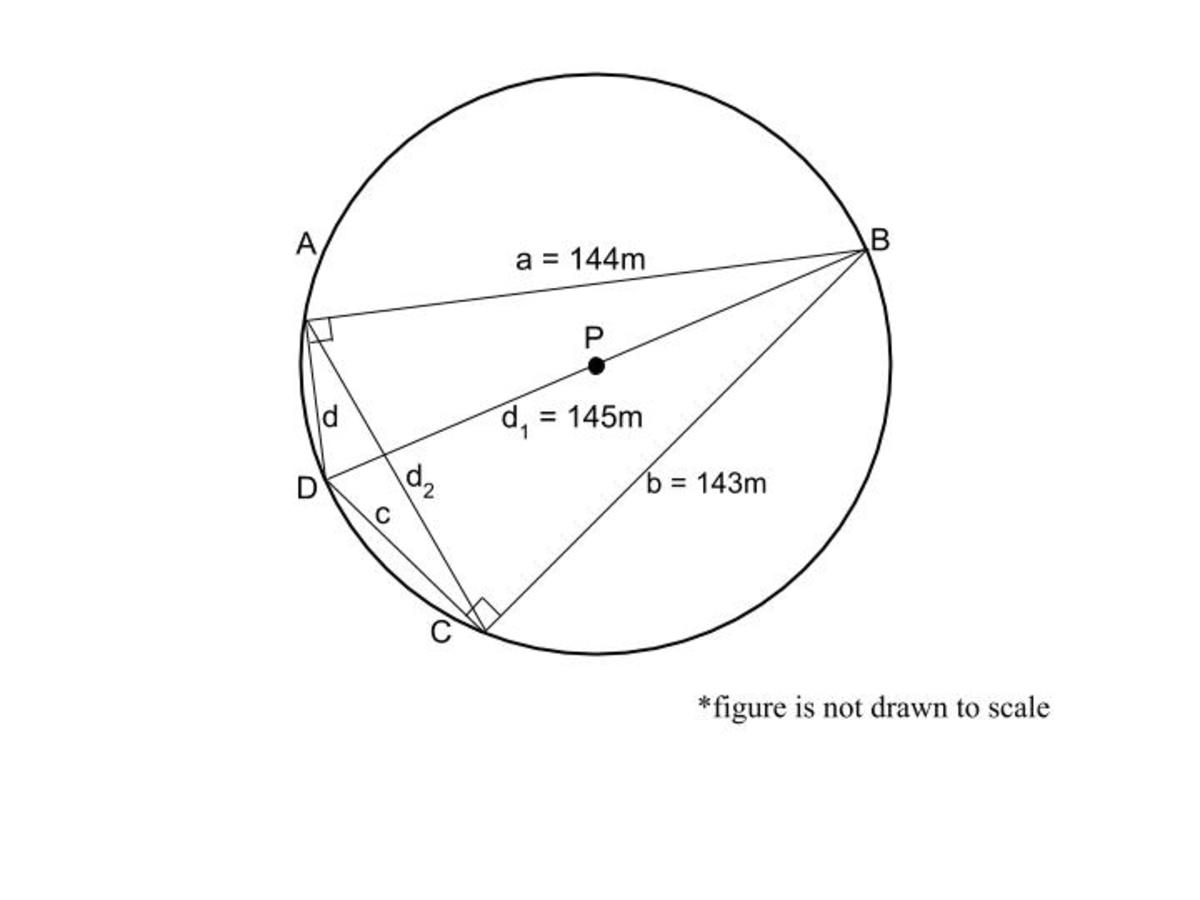
A group of astronomers are trying to observe the rate of change between two separate pairs of planets, where the pairs are not adjacent to one another. A group of planets, planets A, B, C, and D, share the same ring of orbit; therefore, a cyclic quadrilateral is formed. In other words, quadrilateral ABCD is inscribed in circle P. d 1 d_{1} passes through point P. The circumference of circle P increases at a rate of 10π m / s _{m/s} , and the sum of the products of the pairs of opposite sides’ rate of change is 69 6 m / s 696_{m/s} .

Given the equation d 1 d_{1} d 2 d_{2} = ac + bd (where d 1 d_{1} and d 2 d_{2} are the diagonals and a, b, c, and d are side lengths), find the ratio between the rate of change for both diagonals in the form of d d 1 d t \frac{dd_{1}}{dt} : d d 2 d t \frac{dd_{2}}{dt} .

Please refer to the figure below.

List of Givens:

d C d t \frac{dC}{dt} = 10π m / s _{m/s}

(ac + bd) d d t \frac{d}{dt} = 69 6 m / s 696_{m/s}

11:3 2:7 4:9 5:1 8:5

Rachel Taylor by Rachel Taylor , 18, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rachel Taylor
Oct 11, 2020

Solve for d r d t \frac{dr}{dt} :

C = 2𝜋r

d C d t \frac{dC}{dt} = 2𝜋 d r d t \frac{dr}{dt}

10𝜋 = 2𝜋 d r d t \frac{dr}{dt}

d r d t \frac{dr}{dt} = 5 m / s _{m/s}

Solve for d d 1 d t \frac{dd_{1}}{dt} :

2r = d 1 _{1}

2 d r d t \frac{dr}{dt} = d d 1 d t \frac{dd_{1}}{dt}

2(5) = d d 1 d t \frac{dd_{1}}{dt}

d d 1 d t \frac{dd_{1}}{dt} = 10 m / s _{m/s}

Solve for c:

c 2 + 14 3 2 = 14 5 2 c^{2} + 143^{2} = 145^{2}

c = 14 5 2 − 14 3 2 \sqrt{145^{2} - 143^{2}}

c = 24

Solve for d:

d 2 + 14 4 2 = 14 5 2 d^{2} + 144^{2} = 145^{2}

d = 14 5 2 − 14 4 2 \sqrt{145^{2} - 144^{2}}

d = 17

Solve for d d 2 d t \frac{dd_{2}}{dt} :

d 1 d 2 d_{1}d_{2} = ac + bd

d 2 = a c + b d d 1 d_{2} = \frac{ac + bd}{d_{1}}

d d 2 d t \frac{dd_{2}}{dt} = ( d 1 ) ( d d t ( a c + b d ) ) − ( a c + b d ) ( d d 1 d t ) d 1 2 \frac{(d_{1})(\frac{d}{dt}(ac + bd)) - (ac + bd)(\frac{dd_{1}}{dt})}{d_{1}^2}

d d 2 d t \frac{dd_{2}}{dt} = ( 145 ) ( 696 ) − ( 5887 ) ( 10 ) 14 5 2 \frac{(145)(696) - (5887)(10)}{145^2}

d d 2 d t = 2 m / s \frac{dd_{2}}{dt} = 2_{m/s}

Solution:

d d 1 d t : d d 2 d t \frac{dd_{1}}{dt}:\frac{dd_{2}}{dt}

10:2

A n s w e r : 5 : 1 \boxed{Answer: \boxed{5:1}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...