Planks across a ditch part 2
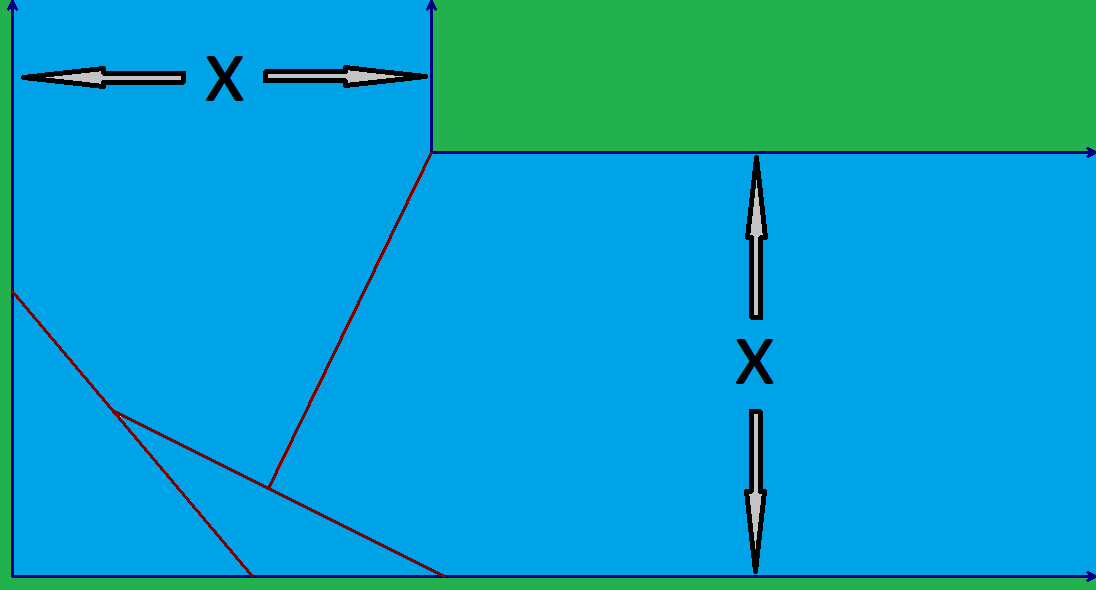
Consider an L-shaped ditch with straight sides and both legs of the same uniform width.
How wide can a ditch be bridged with three 10-foot planks?
Note: consider the planks to be rigid line segments - very thin yet strong. They can only be laid one across another from either side of the ditch.
The answer is 11.32685.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
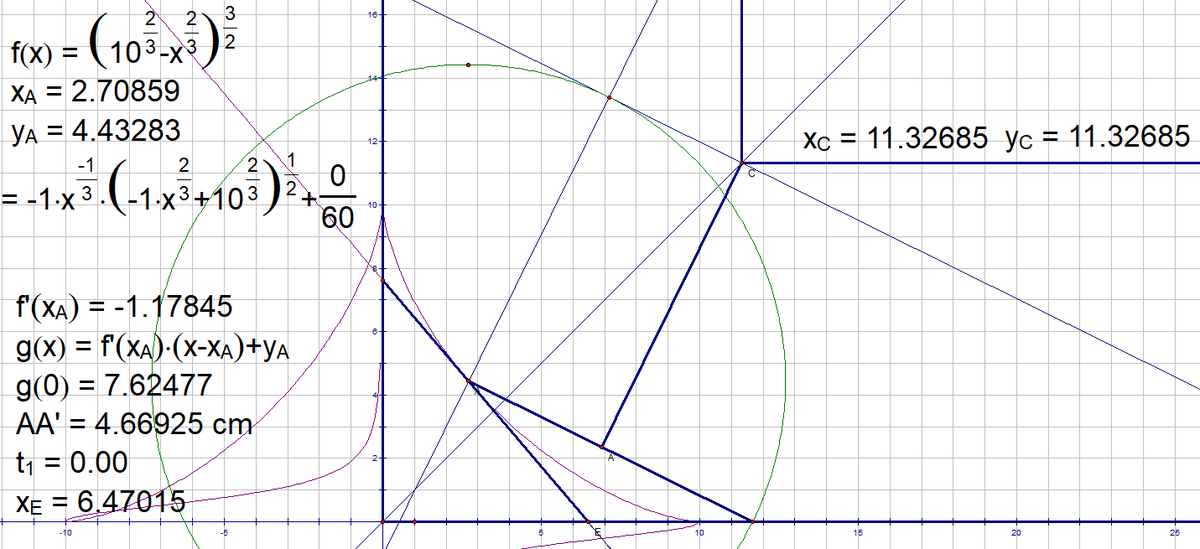
Let the planks be the lines A B , C D , E F , each of length 1 0 , and let B C = x and E D = y , and let ∠ O B A = θ and ∠ O D C = ϕ , while ∠ F E D = 9 0 ∘ .
Then x sin θ = 1 0 sin ϕ , and the coordinates of F are ( X , X ) , where X = ( 1 0 − x ) sin θ + ( 1 0 − y ) cos ϕ + 1 0 sin ϕ = y sin ϕ + 1 0 cos ϕ and hence y X = sin ϕ + cos ϕ ( 1 0 − x ) cos θ + 1 0 sin ϕ = sin ϕ + cos ϕ 1 0 + 1 0 sin ϕ cos ϕ + ( 1 0 − x ) cos θ sin ϕ If we put u = x sin θ and v = ( 1 0 − x ) cos θ we deduce that X = u + 1 0 0 − u 2 1 0 0 + u 1 0 0 − u 2 + u v For the values of x , θ for which X is maximized, we will have ∂ x ∂ X = ∂ θ ∂ X = 0 , and hence 0 = x cos θ ∂ x ∂ X − sin θ ∂ θ ∂ X = [ ( 1 0 − x ) sin 2 θ − x cos 2 θ ] ∂ v ∂ X But it is clear that ∂ v ∂ X = u + 1 0 0 − u 2 u > 0 , and hence we deduce that ( 1 0 − x ) sin 2 θ − x cos 2 θ = 0 , so that x = 1 0 sin 2 θ This then implies that sin ϕ = sin 3 θ and that X = 1 0 sin 3 θ + 1 − sin 6 θ 1 + sin 3 θ 1 − sin 6 θ + sin 3 θ cos 3 θ Maximizing this function of θ numerically over ( 0 , 2 1 π ) , we see that the maximum value of X occurs when θ = 0 . 8 6 6 5 6 6 2 , when X = 1 1 . 3 2 6 8 4 9 .