PlatformSA
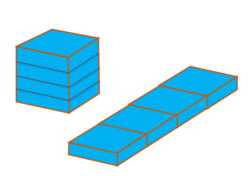 A cubic foot of wood (
) is cut into four pieces, which are made into a platform. What is the external surface area of this platform (including the bottom)?
A cubic foot of wood (
) is cut into four pieces, which are made into a platform. What is the external surface area of this platform (including the bottom)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
SOLUTION 1:
The top and bottom surfaces of the platform each are 1 f t × 4 f t = 4 f t 2 → 8 f t 2 for both.
The two long edge surfaces of the platform each are 4 1 f t × 4 f t = 1 f t 2 → 2 f t 2 for both.
The two short edge surfaces of the platform each are 4 1 f t × 1 f t = 4 2 1 f t 2 → 2 1 f t 2 for both.
So the total SA is 8 f t 2 + 2 f t 2 + 2 1 f t 2 = 1 0 . 5 f t 2
SOLUTION 2:
But my favorite way to see it is to calculate the difference between the original SA of the cube ( 6 f t 2 ) and the new SA. The original cube foot of wood has S A = 6 f t 2 because it has six faces, each 1 f t 2 . Imagine painting it blue and then cutting it up to make the platform.
1) For each of the 3 cuts, 2 new 1 f t 2 surfaces are created/revealed by the cut. That's 6 new f t 2 total.
2) Then, when those 4 pieces are joined together in three places on 1 × 4 1 f t 2 edges, that similarly means 6 of those faces are covered up. 6 × 4 1 f t 2 = 1 . 5 f t 2 lost.
6 f t 2 o r i g i n a l + 6 f t 2 g a i n e d − 1 . 5 f t 2 l o s t = 1 0 . 5 f t 2