Platonic Resistance
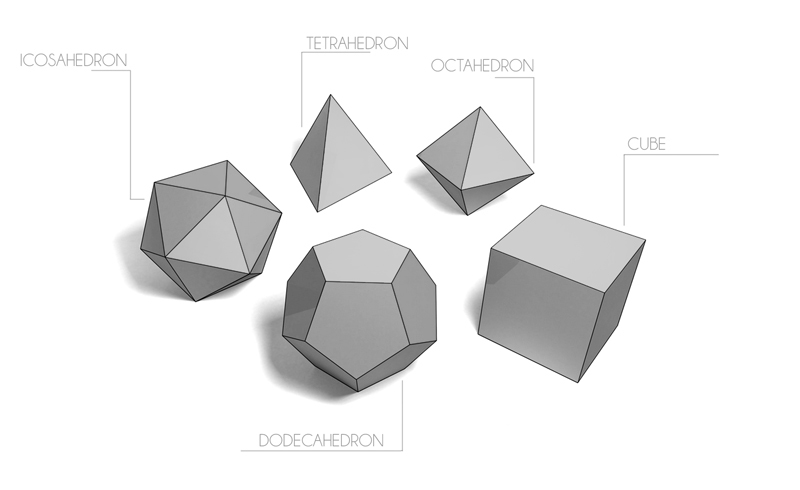
You have each of the five Platonic solids, with edges made out of resistors. For which solid can you pick two vertices that have an effective resistance between them that is greater than ?
Definitions :
-
Tetrahedron is a polyhedron with 4 sides.
-
Octahedron is a polyhedron with 8 flat faces.
-
Dodecahedron is a polyhedron with 12 flat faces.
-
Icosahedron is a polyhedron with 20 flat faces.
-
Oblate spheroid is a quadric surface obtained by rotating an ellipse about its minor axis.
Clarification : "All of these" and "None of these" refer only to the geometrical answers not to each other!
Image credit: http://pixelstains.net/
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the d o d e c a h e d r o n you can get a resistance of 7/6 ohms or 17/15 ohms, by choosing opposite or "nearly opposite" vertices. For all the other Platonic solids, no matter which vertices you pick, the resistance will be less than one ohm. Oh, and an oblate spheroid is not a Platonic solid.
Here is an example for calculating the dodecahedron resistance, and here is one for calculating the icosahedron resistance. If you use a similar technique for the cube, octahedron, and tetrahedron, you'll see that the dodecahedron is the only one for which you can get a resistance that is bigger than the resistance of any given edge.